有限要素法入門
有限要素法とは
有限要素法(finite element method)は,偏微分方程式の近似解を数値的に解く方法のひとつで,構造,伝熱,流体,電磁場などの解析に使用されています。ここでは,弾性体に外力が作用して変形している状態の変位と応力を求める構造分野の有限要素法とその手順を説明します。
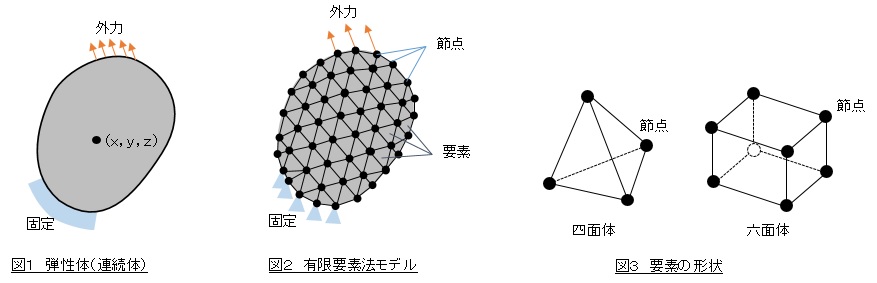
図1に示すような任意の形状の連続体の表面の一部が固定されていて,表面の一部に外力が作用しているときの,任意の点(x,y,z)の変位と応力を弾性力学の基礎方程式を解いて求めるのは,とても難しいことでほぼ不可能と言えます。
そこで,図2に示すように連続体を小さな領域に分割して離散化します。この作業を要素分割とかメッシングと言います。分割した小さな領域を要素(element),要素の端の点を節点(node)と呼びます。要素の形状は図3に示すように四面体や六面体となります。連続体では未知数(変位や応力)は無限個あったのですが,要素と節点に分割することで未知数の数は有限個になりました。
要素の変位は節点の位置の変位で表すことにします。要素に作用する力は節点を介して授受されると考えます。外力は離散化されて節点に作用する力として扱い,固定に関しても節点の変位を拘束するものとして扱います。
要素内の変位は座標の関数ですが,座標の1次式ないしは2次式で変化すると仮定します。そうすると,要素の変位と要素に作用する力の関係について弾性力学的な近似解が求まります。要素の近似解が求まれば全体の近似解も求まります。あくまで近似解ですが,要素分割を細かくすればこの近似解が弾性力学の解に近づくことが期待されます。
弾性体のひずみは変位を座標で偏微分したものであるため,ひずみも簡単に求まります。そして応力はひずみにヤング率を乗じたものなので求まります。
以上が有限要素法の基本的な考え方です。対象物である弾性体を微小な領域に分割することと,微小な領域の中では未知数である変位を座標の簡単な関数として仮定することがポイントです。詳しくは有限要素法詳細を参照してください。
それでは,外力が作用する弾性体の変位と応力を有限要素法で求める手順を説明していきます。
手順1 事前検討
三次元CADで設計して,それを解析しようとしている方が大半だと思いますので,それを前提として説明していきます。設計したモデル全体を解析するのは,要素数と節点数が膨大となりますので避けるべきです。全体モデルから,関心のある部分を取出して解析します。どの範囲を取出すかは難しい問題です。事前検討を十分に行う必要があります。詳しくは事前検討のページで説明します。
手順2 三次元形状モデルの準備
三次元CADで解析対象の三次元形状モデルを作成します。このとき,詳細設計が終わった三次元データをそのまま使えると考えそうですが,有限要素法モデルが複雑になってしまいますので,例えば要素数が膨大となって計算時間がとても長くなってしまいますので,解析に関係ない細かな形状(フューチャー)は除去しておきます。この作業は手間がかかりますがとても重要な作業です。三次元形状モデルの準備のページで詳しく説明します。
有限要素法解析には応力特異点という厄介な問題があります。応力特異点を作らないためと実物が疲労破壊しないようにするために角部にはRをつけておきます。
次に,作成した三次元形状データをSTEP形式やParasolid形式など有限要素法ソフトが読込める形式で出力します。三次元CADに解析機能がつていいる場合はこの作業は不要で,解析機能を立ち上げればOKです。
手順3 三次元形状モデルの読込み
いよいよ有限要素法ソフトを立ち上げます。そして,三次元形状モデルを有限要素法ソフトに読込みます。この作業をインポートと言います。ここで長さの単位に注意が必要です。普通三次元CADでは[mm]単位でモデリングしますが,有限要素法ソフトに読込まれた後の長さの単位が[mm]なのか[m]なのかを確認する必要があります。例えば,長さ10[mm]のブロックを三次元CADでモデリングしてインポートしたとしましょう。有限要素法ソフトがそれを,0.01[m]のブロックとして認識しているか10[m]のブロックとして認識しているか,それとも10[mm]と認識しているかを確認する必要があります。
ヘルプファイルを参照するのも手ですが,自分で確認することを勧めます。例えば答えがわかっている自重が作用する片持ちはりのたわみを手計算で求めておいて,その問題を有限要素法ソフトで計算してみて,両者を比較することで確認します。自重がかかる片持ちはりのページを参考にしてみてください。
手順4 材料定数の入力
ヤング率とポアソン比を入力します。自重を考慮するときは,これらに加えて密度と重力加速度を入力します。インポートされた三次元モデルが[m]単位で有限要素法ソフトに認識されている場合と,[mm]単位で認識されている場合で材料定数の単位が異なります。構造解析で使う材料定数のページ,SI単位系のページ,単位換算方法のページを参考にしてください。
手順5 要素分割
要素分割を行います。メッシングとも言います。線形解析の場合,解析時間と同じくらいの計算時間がかかります。必ず2次要素で要素分割してください。1次要素の使用はもはや時代遅れです。四面体2次要素より六面体2次要素のの方が精度が高いといわれておりますが,四面体2次要素で十分です。要素分割と解析精度のページを参考にしてください。
手順6 境界条件の設定
固定しようと考えている面を固定します。固定に関する注意点は剛体変位の防止と,点や辺を固定するのではなく面を固定することです。変位拘束の注意点のページを参考にしてください。
外力が作用している面に力荷重を設定します。力荷重も点や線に設定するのではなく面に設定するようにします。点荷重と線荷重の禁止のページを参考にしてください。
自重を考慮する場合は,重力加速度とその方向を指定します。
手順7 計算
問題を解きます。最近はウインドウズが64ビット化しメモリを沢山実装できるようになりましたので,線形解析の場合,席を立たないでコンピュータの前に座って待てっている間に計算が終わるでしょう。非線形解析の場合はそういうわけにはいかず,席を立って別の仕事をすることになります。私は一晩で計算が終わるような解析規模になるよう心掛けておりました。
手順8 結果の評価
関心事が強度の場合,相当応力を見ます。くれぐれもレジェンドの最高応力値だけを見て判断しないでください(図4)。応力特異点の応力を見てしまう可能性があります。応力の高い場所を確認しましょう。次に,主応力をみて,その点の応力が引張応力か圧縮応力かを確認します。延性材料で圧縮応力の場合は応力が高くても大丈夫なことが多いです。強度計算をすることになりますが,強度計算のページから読み進めていってください。
関心事が変形量の場合,変形図を表示させます。設計変更して変形量を小さくさせたい場合は,応力の高い場所を見ると設計変更のヒントになります。
モーダル解析を行った場合は,固有振動数と振動モードをみます。設計変更して固有振動数を上げたい場合は,相当応力図を表示させて応力の高いところを見ると,設計変更のヒントになります。

手順9 検証と妥当性の確認
正しく解析できて目的を達成したかを確認します。これをV&V(verification and validation)といいます。少なくとも要素分割の妥当性確認と手計算結果との比較はやっておくべきだと思います。自分自身の創意工夫で解析が正しいものであることを証明し,自分自身と周りの人が納得できるようになるところがポイントです。
プリプロセッサ,ソルバー,ポストプロセッサ
最近のソフトは,プリプロセッサ,ソルバー,ポストプロセッサが一体になったようなユーザインターフェイスになっていますが,歴史のある有限要素法ソフトは,プリプロセッサ,ソルバー,ポストプロセッサが分かれています。上述した手順3,手順4,手順5がプリプロセッサの仕事で,手順6,手順7がソルバーの仕事で,手順8がポストプロセッサの仕事です。また,プリプロセッサで形状モデリングができます。
Information
仮想仕事の原理 を追加しました。


