三軸応力，直交座標系における応力成分

ＨＯＭＥ　＞　材料力学　＞　三軸応力

有限要素法ソフトで表示される応力

有限要素法で応力分布図を表示するとき，いろいろな選択肢があります。以下のようなものです。

• σｘ（ｘ成分垂直応力），σｙ（ｙ成分垂直応力），σｚ（ｚ成分垂直応力），
  τｘｙ（ｘｙせん断応力），τｙｚ（ｙｚせん断応力），τｚｘ（ｚｘせん断応力）

• σ１（第１主応力），σ２（第２主応力），σ３（第３主応力）

• σｅｑ（相当応力，ミゼス相当応力）

最初のσｘ，σｙ，σｚ，τｘｙ，τｙｚ，τｚｘを説明します。

ｘｙｚ直交座標系での応力成分

図１において，物体は左下の方で固定されており，右上のところに外力が作用しているとします。物体内の任意の点(x,y,z)の位置にある小さな立方体を考えます。任意の点の立方体に作用する応力は，立方体の大きさが限りなくゼロに近づいたときの値です。以下のように９個の応力成分があり，物体内の任意の点の応力状態を表現しています。

　σｘｘ，τｘｙ，τｘｚ，τｙｘ，σｙｙ，τｙｚ，τｚｘ，τｚｙ，σｚｚ

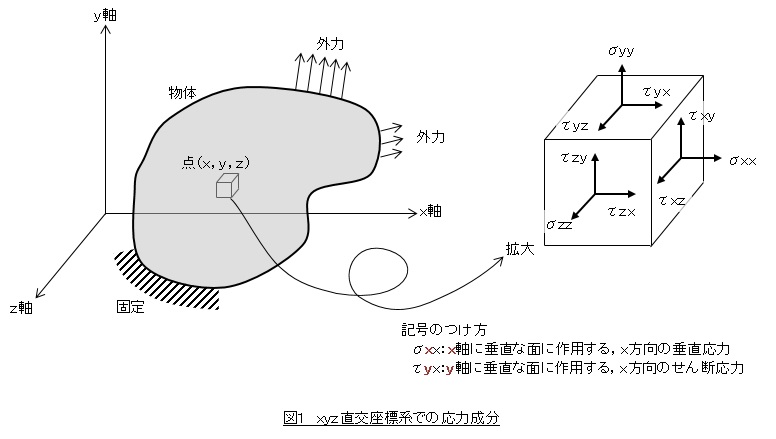
第一の添え字は作用面を表しています。ｘならば作用面の法線がｘ軸と平行であることを意味します。第二の添え字は作用する応力の方向を意味します。σｘｘは，「法線がｘ軸と平行に面に作用する，ｘ方向の応力」です。τｘｙは「法線がｘ軸と平行な面に作用する，ｘ方向の応力」ということになります。

これらの応力は，物体内の任意の位置の座標(x,y,z)の関数なので，σｘｘはσｘｘ(x,y,z)と表現できます。物体は外力によって変形するので，(x,y,z)は変形前の位置か変形後の位置か迷ってしまいそうですが，変形量が微小（微小変形問題）だということでσｘｘ(x,y,z)は変形前の位置(x,y,z)の関数としています。

小さな立方体は静止しているので，そのモーメントのつり合いから，τｘｙ＝τｙｘ，τｙｚ＝τｚｙ，τｚｘ＝τｘｚとなります。便宜上，σｘｘ，σｙｙ，σｚｚをσｘ，σｙ，σｚと表記しましょう。応力成分が以下のように６個となりました。

　σｘ，σｙ，σｚ，τｘｙ，τｙｚ，τｚｘ

応力をマトリクスTで表記することがあります。(1)式となります。これは応力テンソルと呼ばれています。

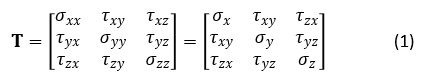
応力をベクトルで表記することもあります。(2)式となります。

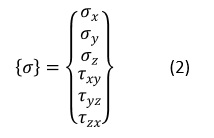
以上が，ｘｙｚ直交座標系での応力成分です。