公称応力と真応力

ＨＯＭＥ　＞　材料力学　＞　公称応力と真応力

公称応力と真応力には２つの意味がある。

公称応力(nominal stress)と真応力(true stress)には以下のように２つの意味があります。

• 応力集中を考慮せずに求めた応力（公称応力）と，応力集中を考慮して求めた応力（真応力）

• 応力の計算において，荷重Ｐを変形前の断面積Ａｏで割って求めた応力（公称応力）と，変形後の断面積Ａで割って求めた応力（真応力）

応力集中の考慮の有無による呼び方の違い

応力集中を考慮せずに求めた応力を公称応力と呼びます。

先端に荷重が作用する片持ちはりを例にして説明しましょう。図１に示したようなすみ肉溶接された片持ちはりのＡ点の応力を求めてみます。長さＬ(25mm)，厚さｈ(10mm)，奥行きｂ(10mm)の片持ちはりの先端に荷重Ｐ(100N)が作用しているとします。

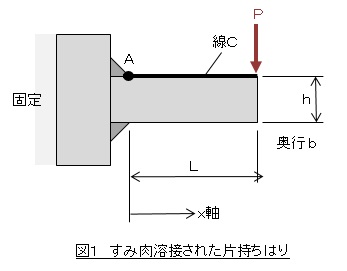
Ａ点の応力σｏは次式で表されます。ここでＭはＡ点の曲げモーメント，Ｉは断面二次モーメントです。長さの単位を[m]に変換して計算しますね。

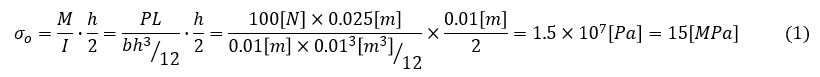
こうやって計算した応力が公称応力です。Ａ点の応力集中を考慮していませんね。この他に材料力学で習った方法で求めた応力は公称応力です。

一方，真応力は，応力集中を考慮して求めた真なる応力です。

有限要素法ソフトを使って求めた線Ｃ上の応力分布を図２に示します。ｘ＝０[mm]近傍で応力が急峻に上がっていますね。これが応力集中です。真応力は図２の青い線で表されます。Ａ点の真応力は38[MPa]となりました。

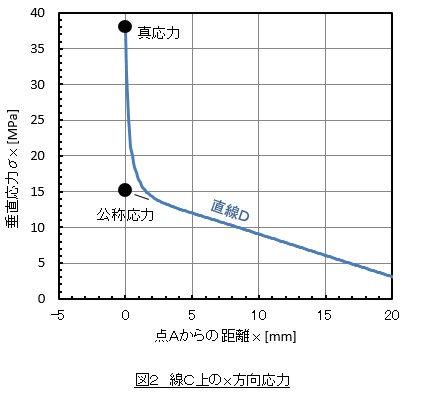
公称応力は図２の青い線をｘ＝０[mm]まで延長することで求まりますが，有限要素法ソフトは公称応力を求めることができません。有限要素法ソフトで公称応力を求めたいときは，ホットスポット応力で代用します。

Ａ点は応力特異点なので応力は無限大なのではと思われたら，その通りです。Ａ点に小さなＲがあるとお考え下さい。

割算した断面積の違いによる呼び方の違い

初期断面積Ａｏ，長さＬｏの丸棒を荷重Ｐで引張ったとします。丸棒は縦方向に長さＬに伸びて，横方向は縮みます。丸棒が変形した後の断面積をＡとします。

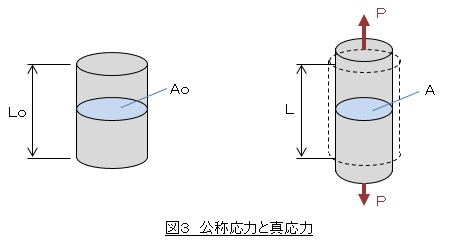
公称応力σｏと公称ひずみεｏ(nominal strain)は次式で定義されています。

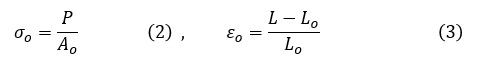
真応力σと真ひずみε(true strain)は次式で定義されています。真ひずみは，自然ひずみ(natural strain)，あるいは対数ひずみ(logarithmic strain)とも言います。

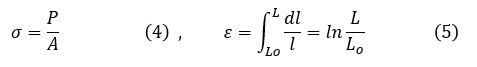
公称ひずみεｏと真ひずみεには，次式の関係があります。

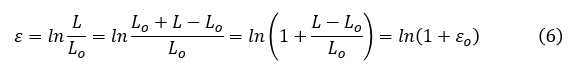
変形が弾性変形ならば引張ったときに丸棒の体積が増えますので成立しませんが，塑性変形の場合は体積が変化しませんので次式が成立します。

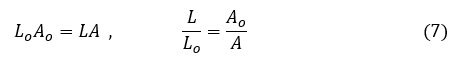
(3)式と(7)式を変形して，公称応力σｏと真応力σの関係を以下のようにして導くことができます。

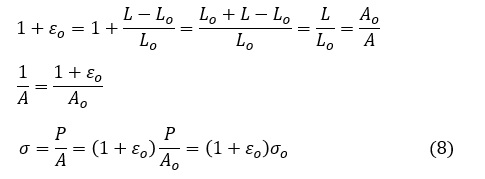
(8)式は，(7)式（体積変化なし）を前提としておりますので，局所的な変形がないとき（例えば引張試験におけるくびれ発生がないとき）に有効です。

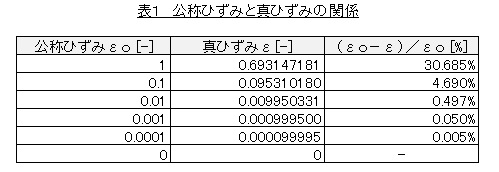
公称ひずみを(6)式に代入して真ひずみを求めたものと，公称ひずみと真ひずみの差[%]を表１に示します。弾性領域（公称ひずみで大体0.001[-]以下）では両者に差はありません。ひずみが0.1[-]を超えるころになると差が無視できなくなります。

弾塑性解析では有限要素法ソフトに応力－ひずみ曲線を入力しますが，そのときは真応力と真ひずみ（ないしは塑性真ひずみ）の関係を多直線近似して入力します。