ホットスポット応力

ＨＯＭＥ　＞　強度計算　＞　応力拡大係数の求め方

ホットスポット応力の必要性

従来の疲労強度評価は，はり理論などにより求まる応力振幅σａ（これを公称応力といいます）と疲労強度σｗを安全率ｆと切欠係数βで割った応力　σｗ／ｆβ　とを比較して，次式が成立すれば大丈夫としてきました。はり理論では応力集中部の応力は求まりませんので，応力集中による強度低下分をσｗをβで割ることにより考慮していたわけであります。この方法は今でも有効な方法で，このサイトでは公称応力ベースの疲労評価と呼んでいます。

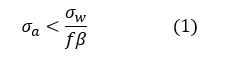
有限要素法により求まる応力振幅は応力集中を考慮した応力として求まりますので，これをασａと表記することにします。αは応力集中係数です。有限要素法ソフトが普及した現在では，ασａと疲労強度σｗを安全率ｆで割った値　σｗ／ｆ　とを比較して，次式が成立すれば大丈夫という考えが広く取り入れられています。これを「真応力ベースの疲労評価」と呼ぶことにしましょう。

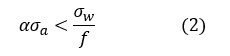
(2)式を変形すると次式となります。

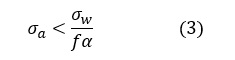
(1)式と(3)式を比較すると　α＝β　となります。つまり，真応力ベースの疲労評価では「βがαと等しい」という前提というか仮定を取り入れています。

この方法では，αが２以下の場合は問題ありませんが，αが２を超える場合は不経済な設計をしてしまう可能性があります。理由を説明します。αが２を超える場合は　α＞β　となります。本来ならば(1)式に従ってσｗをβで割らなければならないのですが，(3)式ではσｗをβより数値の大きなαで割っていますので，許容される応力振幅は小さくなってしまい，本当なら大丈夫な設計が強度不足と判定されてしまいます。この結果，より大きな寸法の設計やより強度の高い材質を採用した設計になって製品コストが上昇します。以上が不経済となる理由です。

それではどうすればいいのでしょうか。公称応力ベースの疲労評価を採用するのでしょうか。しかしここにも問題があります。形状が複雑だと，はり理論を使った手計算で応力振幅を求めるのが困難になります。かといって有限要素法では公称応力が求まりません。このような場合にホットスポット応力（ＨＳＳ）を有限要素法を使って求めて，公称応力の代用とします。

次に，曲率半径ゼロの鋭い切欠やき裂がある場合，弾性力学的には応力が無限大になります。有限要素法でこの点の応力を計算すると要素分割を細かくすればするほどこの点の応力は大きな値として出力され，一義的に決定できません。一方，公称応力ベースで曲率半径ゼロの鋭い切欠やき裂の疲労強度を検討するときには，切欠係数βを３程度にすることにより疲労破壊の有無を予測できます。この検討には公称応力が必要ですが，形状が複雑な場合は手計算で公称応力を求めることができません。このような場合にもホットスポット応力を使います。

ホットスポット応力の定義

ホットスポットは着眼点のことであり，応力集中が激しい点を指します。有限要素法によって求まる応力は，部材の形状により発生する大まかな応力分布σ_Ａと切欠など形状不連続部での応力集中による成分σ_Ｂの和と考えることができます。ホットスポット応力は，応力分布σ_Ａの着眼点での値と解釈しております。単純な曲げ応力が発生している場合は，ホットスポット応力は手計算で求まる公称応力と等しくなり，複雑な応力場の場合には，公称応力自体が計算不可能なのですがもし何らかの手段で公称応力が求まったのなら，ホットスポット応力は公称応力より大きいか等しくなります。

溶接構造物について述べると，ホットスポット応力は構造物の形状やリブなどにより発生する応力分布の着眼点での値であり，溶接ビード止端部の局所的な応力集中成分を含まない応力であるといえます。

ホットスポット応力の求め方

着眼点近傍の応力を有限要素法で求め，それからホットスポット応力を求めます。２点外挿法と１点代表法があります。２点外挿法は，着眼点から板厚の0.5倍の距離の応力と1.5倍の応力を直線で結び，着眼点の位置の応力を外挿して求めます。これを「SR202 B法」と言います。１点代表法は着眼点から板厚の0.3倍の距離の応力をホットスポット応力とします。これを「0.3ｔ法」と言います。これらを図１に示します。簡便性から私は0.3ｔ法を使っています。

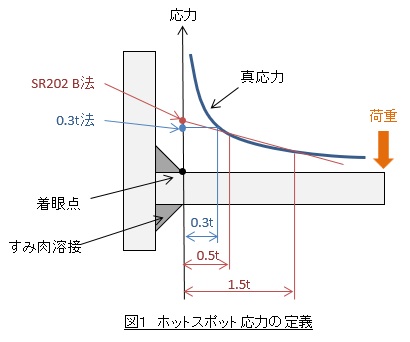
図１を見ると0.3ｔ法による値がSR202 B法による値より小さく見えますが，そうなることもあれば同程度の値となることもあります。

ホットスポット応力は，有限要素法で求めるだけでなくひずみゲージを使って実験的に求めることもできます。

計算例

図２のような溶接接手の公称応力とホットスポット応力を求めてみましょう。公称応力ははり理論で求まって，30 [MPa]です。

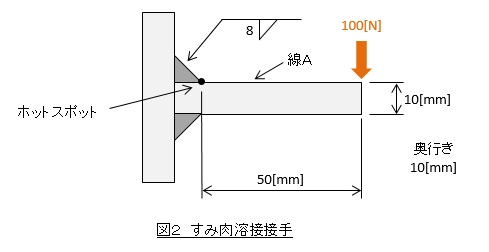
図３に有限要素法ソフトによる応力解析結果を示します。ホットスポットであるＢ点で応力集中が発生しています。

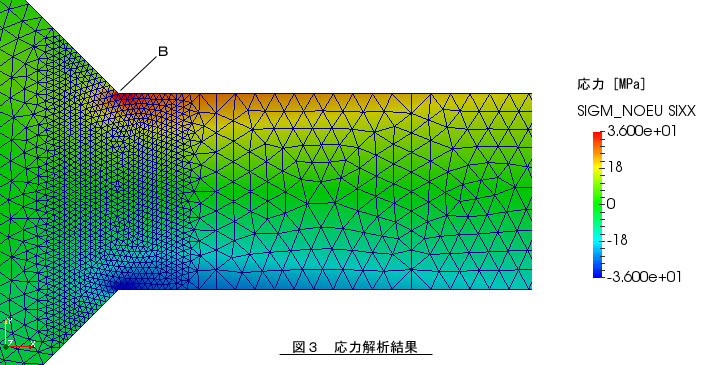
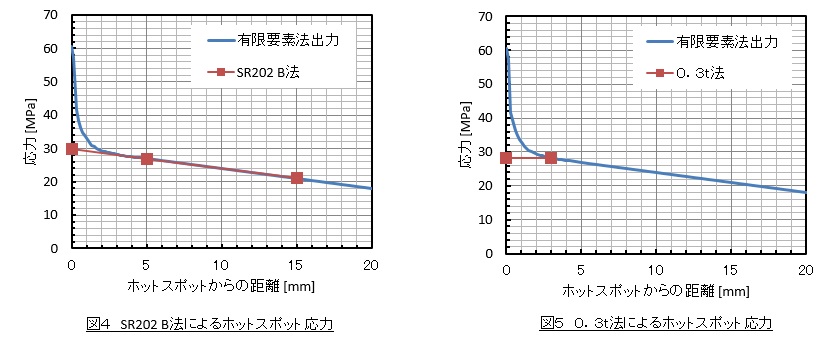
図４は，図２の線Ａ上の水平方向応力分布とSR202 B法によるホットスポット応力です。ホットスポット応力は29.86 [MPa]になり，公称応力とほぼ等しくなりました。図５は０．３ｔ法によるホットスポット応力です。ホットスポット応力は28.20 [MPa]となり。これも公称応力とほぼ等しくなりました。このように，ホットスポット応力は公称応力とほぼ等しく，形状が複雑ではり理論などによって公称応力が求められない場合に，公称応力の代用にすることができます。

参考文献

１）日本溶接協会フェブサイト，http://www-it.jwes.or.jp/qa/details.jsp?pg_no=0040020190

２）（社）日本鋼構造協会，鋼構造物の疲労設計指針・同解説，技報堂出版，(2004)