疲労限度線図

ＨＯＭＥ　＞　強度計算　＞　疲労限度線図

疲労破壊するかしないかの限界線

図１は疲労試験時の応力変化で，最大応力σｍａｘ，最小応力σｍｉｎと平均応力σｍ，応力振幅σａの関係を示します。鉄鋼材料ではＳ－Ｎ曲線に疲労限度が現れます。疲労試験で平均応力σｍを変化させていったとき，疲労限度がどのように変化するかを述べます。日本で初めて疲労限度線図を紹介したと推測される論文¹⁾のデータを使って説明します。

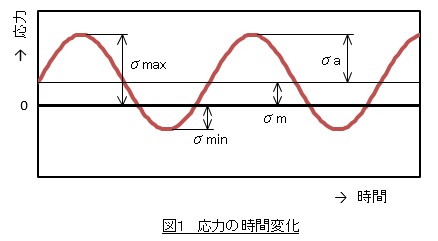
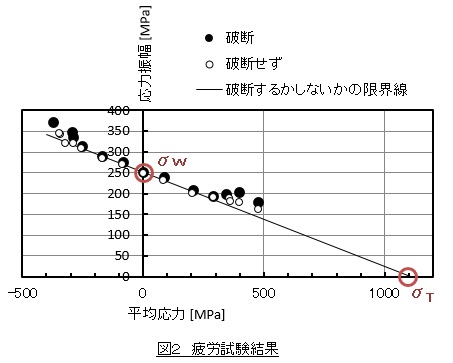
試料は炭素濃度が0.4%Cの炭素鋼で，引張り強さσ_Ｂは696[MPa]，降伏応力σｙは382[MPa]，両振り疲労限度σｗ（平均応力がゼロのときの疲労限度）は251[MPa]，真破断応力σ_Ｔ（引張試験で試験片が破断したときの荷重を破断後の断面積で割った値）は1107[MPa]でした。

図２は，平均応力σｍを変化させて疲労限度を調べた結果です。黒丸プロット（●）が破断したデータ，白丸プロット（○）が破断しなかったデータです。黒丸プロットと白丸プロットの中間を結んだ線が疲労破壊するかしないかの限界線で，１本の直線になりそうです。この限界線は，平均応力が大きくなるにつれて疲労限度は低下することを示しています。プラスの応力は引張応力，マイナスの応力は圧縮応力ですので，引張の平均応力が大きくなると疲労限度が低下します。

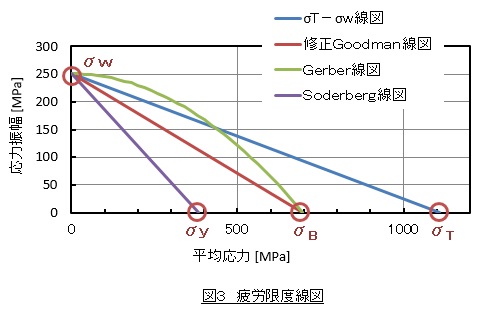
横軸（平均応力の軸）の切片を真破断応力σ_Ｔとし，縦軸（応力振幅の軸）の切片を両振り疲労限度σｗとして直線を引くと，疲労破壊するかしないかの限界線と一致します。縦軸を応力振幅とし横軸を平均応力として，この限界線を描いた図を疲労限度線図（fatigue limit diagram）と言います。

いろいろな疲労限度線図

上述した疲労限度線図はσ_Ｔ－σｗ線図と呼びますが，その他にもいくつかの疲労限度線図が提案されています²⁾。それらを図３に示します。平均応力σｍと応力振幅σａの関係式を以下に記します。

設計に使う疲労限度線図

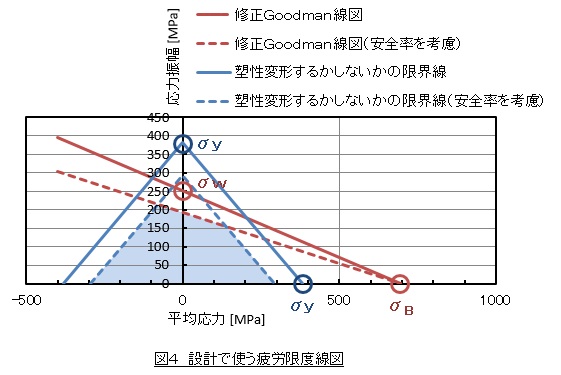
仕事では私は修正Ｇｏｏｄｍａｎ線図を使っています。機械の設計では部品が疲労破壊しないことと塑性変形しないことの両方を考慮する必要があります。塑性変形するかしないかの限界線を図４の青色の実線に示します。塑性変形するかしないかの限界線は，横軸の切片を降伏応力σｙ，縦軸の切片も降伏応力とした直線です。安全率を考慮しなれけばなりませんので，切片を降伏応力／安全率とした線（青色の破線）を引きます。次に修正Ｇｏｏｄｍａｎ線（赤色の実線）と安全率を考慮した修正Ｇｏｏｄｍａｎ線（赤色の破線）を引きます。設計で使用可能な応力範囲は，青色の破線と赤色の破線に囲まれた水色で着色した領域になります。

疲労限度線図を使った計算例は，繰返し荷重が作用する場合と公称応力ベースの疲労評価のところで紹介しています。

参考文献

１）西原，櫻井，繰返引張圧縮應力を受ける鋼の強さ，日本機械学會論文集，(S14)

２）日本機械学会，機械工学便覧　基礎編　Ａ４　材料力学，丸善，(1992)