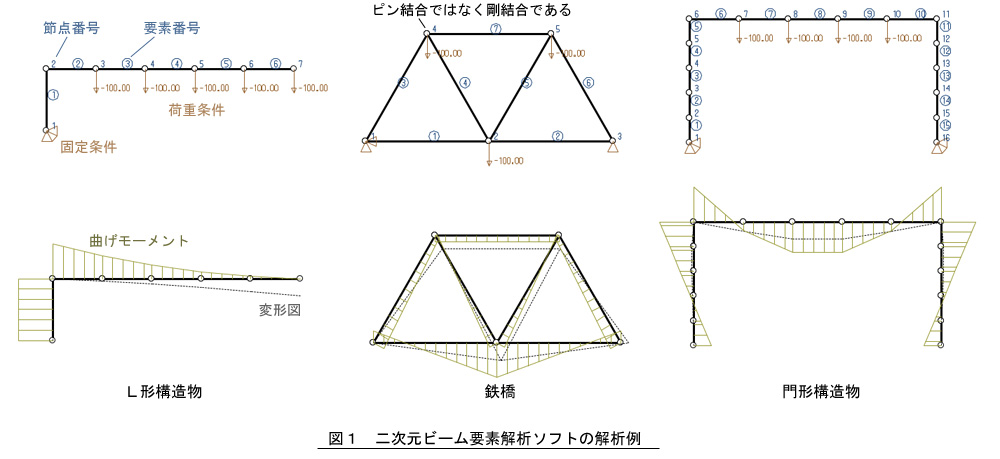
二次元ビーム要素解析ソフト

ＨＯＭＥ　＞　フリーソフト　＞　二次元ビーム要素解析ソフト

ダウンロード

二次元ビーム要素解析ソフトです。いわゆるラーメン構造物の解析ソフトです。要素と要素の結合はピン結合ではなく剛結合（曲げモーメントを伝達）です。図１に示すように，節点と要素を定義し，固定条件と荷重条件を設定するだけで，変形図と曲げモーメント図を表示し，図２に示すように各節点の変位，軸力，せん断力，曲げモーメント，および，応力を出力します。

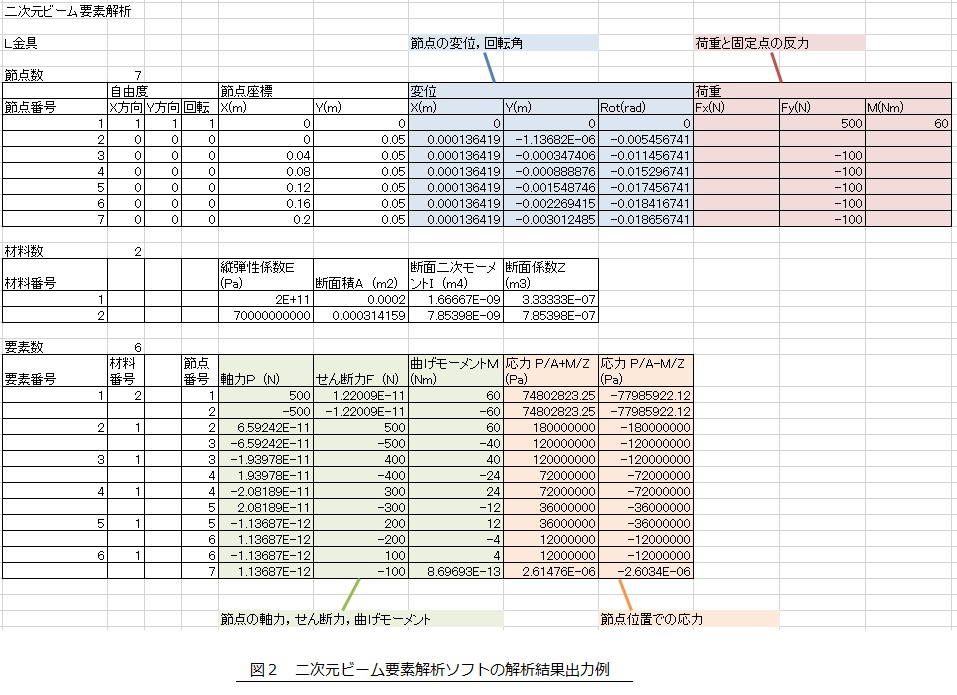
出力される応力について図３を使って説明します。各要素には軸力と曲げモーメントが作用します。軸力Ｐによって軸方向応力Ｐ／Ａが発生します。ここでＡは要素の断面積です。そして，曲げモーメントＭによって曲げ応力±Ｍ／Ｚが発生します。ここでＺは断面係数です。曲げ応力は片側が引張応力ならばその反対側は圧縮応力なので，プラスマイナス（±）Ｍ／Ｚと表現しました。

出力される応力はこれらの和であり，ひとつめの応力はＰ／Ａ＋Ｍ／Ｚ，ふたつ目の応力はＰ／Ａ－Ｍ／Ｚとなります。プラスの応力値は引張応力，マイナスの応力値は圧縮応力を表します。

ソフトの使い方

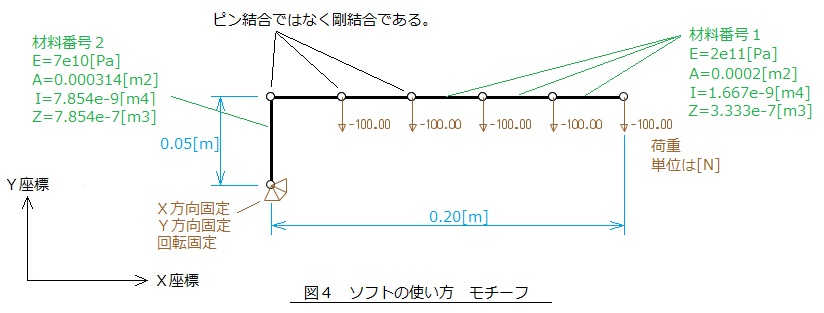
図４に示すようなＬ形の片持ちはりの変位と応力を求めてみましょう。図のＥ，Ａ，Ｉ，Ｚは，それぞれヤング率，断面積，断面二次モーメント，断面係数です。

断面二次モーメントと断面係数は，別のフリーソフト断面二次モーメント計算ソフトで求めることができます。

手順１　ソフトのダウンロード

「ダウンロード」をクリックして，ソフトをダウンロードをしてください。ソフトはマクロ付きエクセルファイルでそのファイル名は「2d_beam.xlsm」です。

ダウンロード

ダウンロードファイルはzip形式で圧縮されていますので，解凍してください。

下図に示すようにセキュリティの警告が出ますので，「コンテンツの有効化」をクリックしてください。

手順２　節点の設定

図５のように，紙に節点番号と節点座標を書きます。そして，節点の固定条件を決めます。今回の場合は，節点１のＸ方向変位の固定，Ｙ方向変位の固定，回転固定，です。

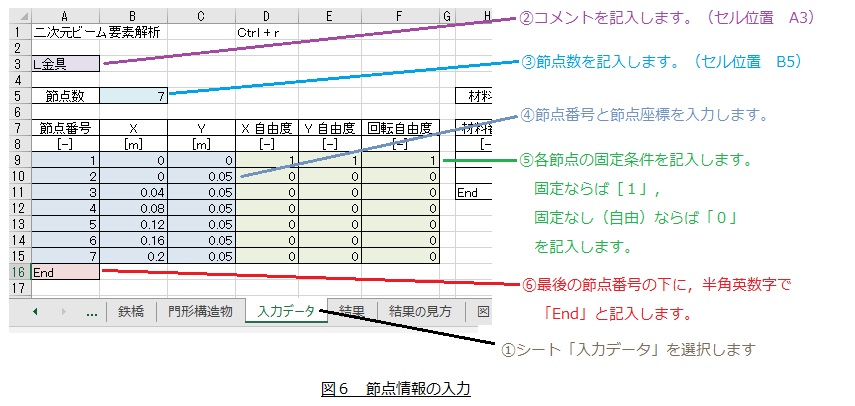
エクセルの中で，シート「入力データ」を選択します。

図６の説明に従って節点情報を入力します。Ｘ自由度，Ｙ自由度，回転自由度について説明します。今回の場合は，節点１のＸ方向変位の固定，Ｙ方向変位の固定，回転固定なので，節点１のＸ自由度，Ｙ自由度，回転自由度に「１」を入力します。他の節点（節点番号２～７）は固定しませんので，Ｘ自由度，Ｙ自由度，回転自由度に「０」を入力します。

そして，最後の節点番号の下に半角英数字で「End」と記入します。これの記入を忘れるとエラーメッセージが出ますので，忘れずに入力してください。

手順３　材料定数の設定

図７の説明に従って材料定数を入力します。今回の場合は２種類の材料を使いますので材料数は「２」を入力します。そして，それぞれの材料に対して材料番号（１と２）をつけます。そして，ヤング率Ｅ[Pa]，断面積Ａ[m²]，断面二次モーメントＩ[m⁴]，断面係数Ｚ[m³]，を入力します。

そして，最後の材料番号の下に半角英数字で「End」と記入します。

手順４　要素の定義

図８に示すように，要素に番号をつけます。要素番号は丸数字（①②③④⑤）で記入することが決まりです。

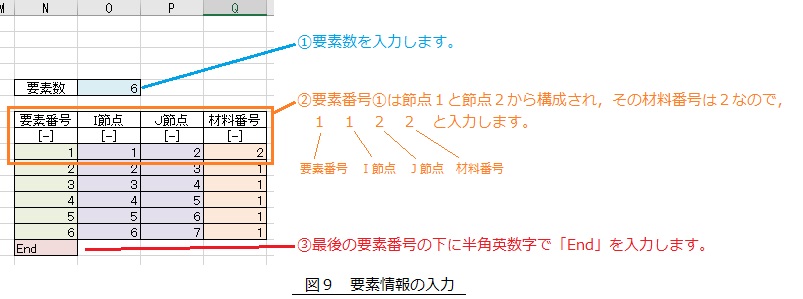
図９の説明に従って要素情報を入力します。

まず，要素の数は全部で６個なので，要素数に「６」を入力します。

今回の場合，要素番号①は節点１（Ｉ節点）と節点２（Ｊ節点）から構成され，その材料番号は２なので，図のオレンジ色で囲った部分に　１　１　２　２　と入力します。次に，要素番号②は節点２（Ｉ節点）と節点３（Ｊ節点）から構成され，その材料番号は１なので，その下の行に　２　２　３　１　と入力します。この要領で要素番号⑥まで入力します，

そして，最後の行に半角英数字で「End」を入力します。

手順５　荷重条件の定義

図10に荷重条件を示します。

図１１の説明に従って荷重条件を入力します。

今回は，節点 3, 4 ,5, 6, 7 に荷重が作用しているので荷重数のセルに「５」を入力します。節点は全部で７つありますが，緑色の荷重条件の入力欄には荷重が作用している節点だけ入力するので，５行になります。

節点 3, 4, 5, 6, 7 にＹ方向荷重 -100[N]が作用しているので，Ｙ方向荷重のセルに「-100」を入力します。Ｘ方向荷重はありませんので 0[N]を入力します。モーメント荷重も作用していませんので 0[Nm]と入力します。モーメント荷重は反時計回りがプラス値です。

手順６　解析の実行

いよいよ計算を開始します。

図１２に示すように，エクセルのメニューにて「表示」をクリックし，「マクロ」／「マクロの表示」をクリックします。

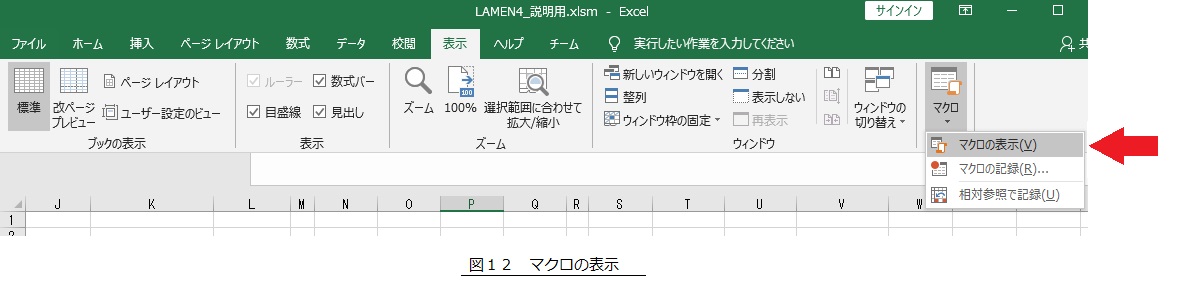
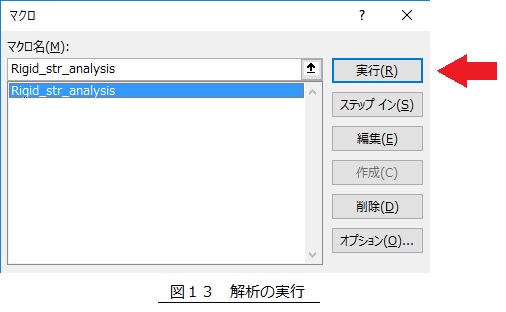
図１３に示すように，「Rigid_str_analysis」を選択し「実行」ボタンを押します。

ショートカットキーで解析を実行させることもできます。入力モードを「かな漢字変換」ではなく「半角英数字入力」にして，「Ctrl」キーを押しながら「R」キーを押します。

手順７　結果の表示

図１４に示すように，順に４つのダイアログボックスが表示されますので，図示したように選択します。

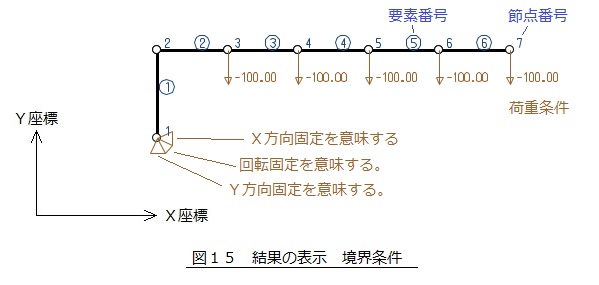
図１５に示すような結果が表示されます。

もう一度，手順６に従って解析を実行します。今度は図１６のように選択します。

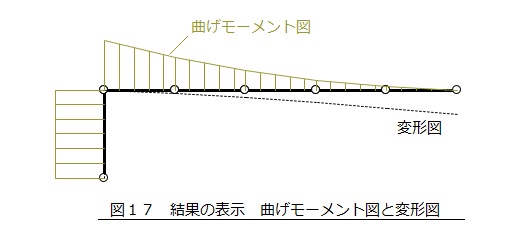
図１７に示すような結果が表示されます。

エクセルシート「結果」を選択すると，図２のような解析結果が表示されます。

要素分割について

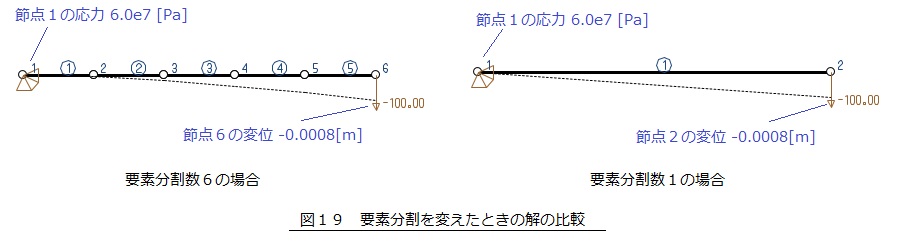
はり理論の解を出力しますので，要素分割を細かくする必要はありません。図１９に示すように，要素分割が１分割でも，細かくしても結果は変わりません。節点は，固定したいところ，荷重が作用するところ，変位や応力などの結果がみたいところに設定します。