強度計算

ＨＯＭＥ　＞　強度計算　＞　強度計算

設計した機械の部品が破損するかどうかを，設計段階で予測することを強度評価と呼び，判断基準となる物理量を強度評価パラメータと言います。破損としては，「部品の破壊」，「塑性変形して使い物にならないこと」，「疲労破断」，「き裂発生」などがあります。疲労については，高サイクル疲労と低サイクル疲労があります。

もし部品にき裂が発生していたら，その部品は破損したと判断して部品を交換し，き裂発生は強度計算が不十分だったとして設計をやり直します。一方，き裂の存在を許容し，そのき裂が機械の使用期間（何年とか何十年とかになります）で破断に至らなければよしと判断する場合もあります。このような場合はき裂の進展速度の計算が必要になります。

強度評価の代表例として，設計段階で計算した応力σと材料の引張強さσ_Ｂとの比較があります。「σ＜σ_Ｂならその部品は破断しない。」という判断を下すことになります。

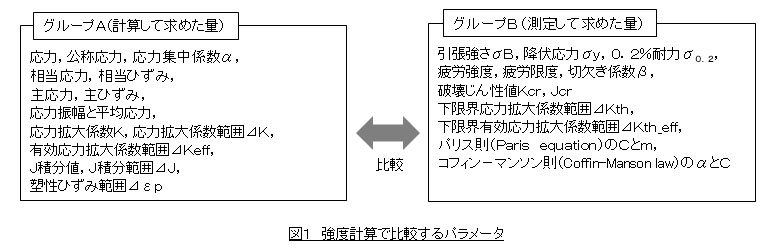
実はここで二つの物理量（パラメータと呼んでもいいと思います）が登場します。一つ目は「設計段階で計算した応力σ」です。この種のパラメータをグループＡと呼びましょう。グループＡの特徴は，何らかの方法で計算して求めたパラメータであることです。有限要素法の出番ですね。二つ目は「材料の引張強さσ_Ｂ」です。この種のパラメータをグループＢと呼びましょう。グループＢの特徴は，何らかの試験で測定した量で材料の機械的性質つまり物性値であることです。

強度評価では，グループＡとグループＢの大きさを比較して，部品の破損の有無を予測します。繰返しになりますが，もっとも簡単な例では，「グループＡの計算した応力σ（グループＡ）が，σ_Ｂ（グルーブＢ）より小さければ破損しない。」と判断することがあげられます。グループＡとグループＢを図１に示します。沢山ありますね。

以上のように，強度計算は奥深く広範囲にわたるもので，浅学の私にはすべてを述べることはできませんが，本サイトでは私が今までメカ設計者として経験したことを中心に説明していきます。

もっとも基本的な強度評価は，機械や構造物が破損するかしないかを，材料にかかる負荷の大きさの指標である「応力」と呼ばれるパラメータを使って判断します。応力のかかり方で分類すると以下のようになります。

• 静荷重が作用する場合
  　有限要素法ソフトで応力解析をした場合，ほとんどが６つの応力成分（σｘ，σｙ，σｚ，τｘｙ，τｙｚ，τｚｘ）すべてが同時に作用する結果となります。 相当応力や主応力を使用して破損の有無を予測します。

• 繰返し応力が作用する場合
  　６つの応力成分すべてが時間の経過とともに変化する場合です。 機械や構造物の一生の間に作用する繰返し荷重の回数が１０^４～１０^５回を境にして，低サイクル疲労と 高サイクル疲労に分類されます。 高サイクル疲労のことを単に疲労と呼ばれています。ここでは高サイクル疲労の場合の強度評価方法を説明します。主応力を使用して疲労破壊の有無を予測します。

疲労破壊は応力集中部や材料欠陥のある場所から発生します。応力集中は部品の形状と密接な関係があります。対象物の形状で分類すると以下のようになります。

• 単純な形状の場合
  　設計した部品が応力集中を起こすような切欠きを持たなくても，形を持つ以上応力の高い部分と低い部分があるはずです。手計算や有限要素法ソフトで応力を求めます。静荷重が作用する場合や繰返し荷重が作用する場合を参照してください。

• 切欠を持つ場合
  　応力集中を起こすような切欠きを持っている場合，手計算で公称応力を求めてそれに応力集中係数αを乗じて応力を求めたり，有限要素法ソフトで応力集中部の要素分割を十分細かくして応力を求めます。静荷重が作用する場合や繰返し荷重が作用する場合を参照してください。

• き裂や曲率半径ゼロの凹状の角を持つ場合
  　き裂や激しい応力集中を起こすような曲率半径ゼロの切欠きを持っている場合， 応力集中係数αが無限大になり，このような点を応力特異点と言って有限要素法ソフトで正確な応力を求めることができません。 応力拡大係数を求めてき裂の進展の有無を予測することになります。 もしくは，曲率半径ゼロの切欠の切欠係数βが３～４であることを利用して，公称応力ベースの疲労評価を行うことになります。

ひとつづつ説明していきます。