Ｌ金具問題

図１にＬ金具を示します。この金具がそう簡単に壊れないことは誰もが知っています。角部の強度について考察したいと思います。この場では，角部の曲率半径ρ（コーナＲ）はゼロ[mm]とします。

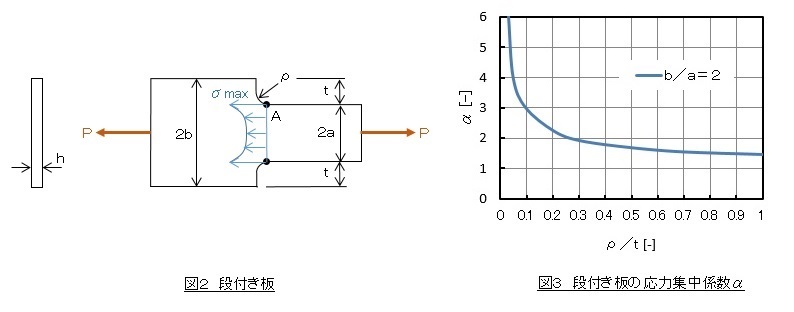
角部の応力集中係数αを求めてみましょう。Ｌ金具のデータはありませんでしたので図２に示すような段付き板に引張り荷重Ｐが作用している場合を例にとります。段の部分には曲率半径ρのコーナＲがあるとします。最大応力σ_ｍａｘはＡ点近傍で発生します。応力集中係数αは図３のようになります。

今回は角部の曲率半径ρがゼロの場合です。応力集中係数αは無限大となります。図２に示すような段付き板に限らず，曲率半径ρがゼロ[mm]の場合はどのような形であっても応力集中係数αは無限大となります。よって，Ｌ金具の角部の応力は無限大となります。

Ｌ金具の角部の応力が無限大なのでほんの小さな荷重を加えたらＬ金具は壊れてしまうのでしょうか。違いますね。そう簡単に金具は壊れませんね。繰り返し荷重の場合どうでしょうか。荷重の大きさにもよりますが，この場合もそう簡単に角部からき裂が進展しませんね。なぜでしょう。

Ｌ金具がガラスでできている場合はどうでしょうか。ガラスはガラス切りでほんの小さな傷を入れただけで簡単に割れてしまうので，Ｌ金具（Ｌガラスですね）は金具より小さな荷重で割れてしまうでしょう。でも割れる荷重はゼロではありません。

Ｌ金具が金属であってもガラスであっても，ほぼゼロのほんの小さな荷重で壊れないのはなぜでしようか。有限要素法を使ったら答えが出てくるのでしょうか。応力特異点問題となって応力が求まらないでしょう。この答を探すために，いろんな人と議論したり，また自分なりに考えてみました。

１回限りの荷重の場合と繰返し荷重の場合に分けて考えてみます。

１回限りの荷重の場合　グリフィス理論による説明

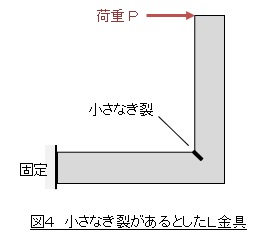
図４に示すように，角部に小さなき裂がすでにあるとします。き裂が進展するかしないかの限界荷重をＰとします。角部の応力が無限大なのでＰの値はゼロ近傍になってしまいそうですが，問題はＰがゼロ近傍かある一定の大きさの値となるかです。ある一定の大きさであるとすれば，Ｌ金具がそう簡単に壊れない説明になりますね。

き裂が進展するとき表面積が増えますが，表面積を増やすためにはエネルギが必要なのです。これがＰがゼロ近傍の値ではなくある大きさを持つ理由です。もう少し詳しく説明しましょう。

き裂の長さをaとします。長さaのき裂を生成するのに要したエネルギは次式で表されます。ここでＬ金具の板厚を１とします。そしてき裂には上面と下面があるので２倍しています。

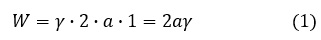
ここでγは表面エネルギとか表面エネルギー密度と呼ばれている量で単位は[J/m²=N/m]です。単位から推察すると表面張力のような物理量と解釈しております。

き裂を単位長さ（今回の場合1[m]）だけ進展させるのに要するエネルギは次式で表されます。

き裂を微小量Δｘでけ進展させるのに要するエネルギΔＷは次式で表されます。

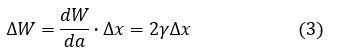
一方，Ｌ金具には荷重Ｐによって応力とひずみが発生しているので弾性エネルギが蓄えられています。この量をＵとします。Ｕはき裂長さａと荷重Ｐの関数となります。き裂が進展するとこの弾性エネルギは解放されて小さくなります。単位長さだけき裂が進展したときの弾性エネルギの減少量をdU／daとします。この弾性エネルギの減少量は何かのために消費されます。き裂が進展するのにエネルギが必要と述べましたね。これに消費されます。

き裂がΔｘだけ進展したときに解放されるエネルギΔＵは次式で与えられます。

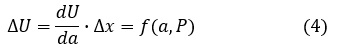
解放されるエネルギΔＵが必要とするエネルギΔＷより少なければき裂は進展しません。解放されて供給されるエネルギΔＵが十分大きく必要とするエネルギΔＷより大きければき裂は進展します。き裂進展の条件は次式となります。

(5)式に(3)，(4)式を代入すると次式となります。これがグリフィスの条件式です。

(5)式に(3)，(4)式を代入すると次式にもなります。

ｆ（ａ，Ｐ）はａとＰに比例するので，比例定数をＫとして次式で表すことができます。

γはガラスで１[J/m²]程度なので¹⁾，(8)式からＰはゼロではないある大きさの値を持つことになります。つまり，応力集中係数が無限大であっても，簡単に壊れるのではなくある大きさの値を持つ荷重Ｐを与えなければ壊れないことになります。

以上が１回の荷重に対してＬ金具がそう簡単に壊れない説明となります。

図４は説明のために私が勝手に作ったもので，グリフィス理論では中央にき裂がある平面応力状態の無限平板で，変位一定の引張荷重であることを前提としています。(1)，(2)，(3)，(4)，(5)，(7)，(8)式も説明のために私が勝手に作った式です。グリフィス理論ではき裂の長さは２ａなので(1)式は　Ｗ＝４ａγ　です。

アーウィンによる修正

Ｌ金具問題とは話がそれますがアーウィンによる修正に触れておきます。

上述したグリフィスの理論はガラスのような脆性材料では実験データとよく一致しました。しかし金属のような延性材料では一致せず，き裂を進展させるのに要するエネルギーは何桁も大きいものでした。この理由は図５によ示すように荷重が作用したときに小規模な塑性変形が生じているからです。図５の塑性変形領域は大きく書いています。実際はもっと小さな領域でしょう。

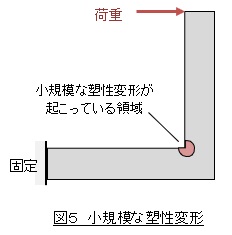
アーウィンらは，き裂が進展することによって生じた弾性エネルギの減少分は，(A)き裂によって表面を広げるために消費される（表面エネルギγ）のと，(B)き裂先端の塑性変形のために消費される（塑性ひずみエネルギーγ_p）と考えました。(B)の多くは最終的に熱となって拡散します。そして，グリフィスの式に塑性ひずみエネルギーγ_pの項を入れて，き裂進展の条件式としました。

話をＬ金具問題に戻しましょう。１回限りの荷重ではＬ金具を壊すのにはある大きさの荷重Ｐが必要なことは説明できました。それでは繰返し荷重の場合もＬ金具が疲労破壊する荷重振幅Ｐはゼロに近い値ではなくある大きさとなるのでしょうか。２つの考え方で説明していきます。

繰返し荷重の場合　公称応力と切欠係数βを使った説明

角部の公称応力を求めてみましょう。図６にＬ金具の寸法，図７に荷重の時間変化を示します。荷重は両振荷重で振幅をＰとします。

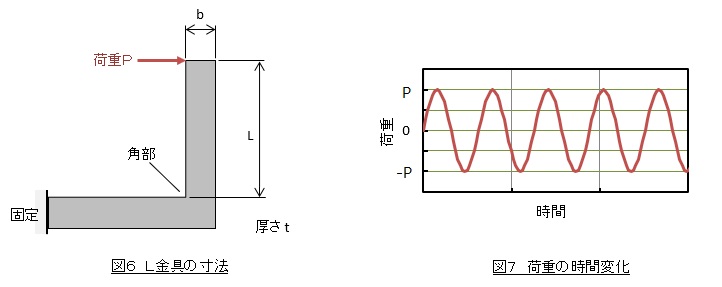
応力振幅σ_ａは次式で表されます。

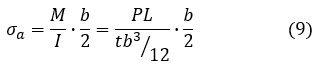
金具は鉄鋼材料でできており疲労限度σ_ｗが現れるとします。疲労破壊しない条件は次式となります。

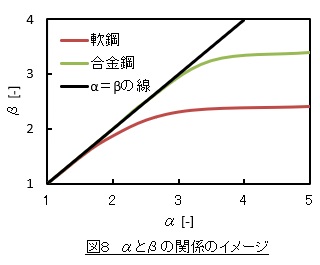
ここでβは切欠係数です。βの値をいくらにするのかが問題です。角部の応力が無限大なのでβも無限大なのでしょうか。図８に応力集中係数αと切欠係数βの関係を示します。αが小さいときはα＝βですがαが大きくなるとα＞βとなり，αがもっと大きくなるとβは一定の値（２～３）に収れんします。つまりαが無限大のときβは有限の値（２～３）になります。この結果，(10)式の右辺がゼロでなくなってゼロでない応力振幅σ_ａが存在することになります。

σ_ａとＰは比例関係にあるので，曲率半径がゼロ[mm]であっても疲労破壊しない繰返し荷重Ｐが存在することになります。以上が疲労破壊しない説明です。

繰返し荷重の場合　破壊力学を使った説明

破壊力学を使って曲率半径がゼロ[mm]であっても疲労破壊しないことを説明してみましょう。図４に示すように角部に小さなき裂がすでに発生していると考えます。

荷重が作用したときのき裂先端の応力拡大係数Ｋを求めます。Ｌ金具のき裂なんて公式集には載っていないので有限要素法の出番となりますね。荷重Ｐは繰返し荷重であるので応力拡大係数範囲ΔＫが求まります。ＰとΔＫは比例関係にあります。

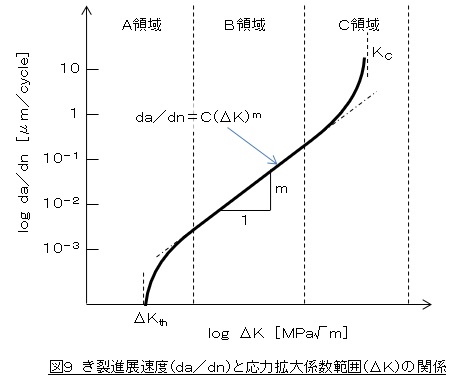
今，荷重１サイクル当たりのき裂進展量をｄａ／ｄｎと表記します。ｄａ／ｄｎをき裂進展速度（fatigue crack propagation rate）と呼び，その単位は［μm／cycle］です。荷重振幅Ｐが大きいときはΔＫが大きくなりき裂がどんどん進展してｄａ／ｄｎが大きくなること，反対にΔＫが小さいときはき裂の進展量も小さくなってｄａ／ｄｎが小さくなることは想像できますね。ｄａ／ｄｎとΔＫの関係を両対数グラフで表すと図９のようになります。

図９のＢ領域において，両対数グラフで表したときにｄａ／ｄｎとΔＫの関係が直線になります。これはパリス則と呼ばれています。領域Ａに注目します。ΔＫを小さくしていくとｄａ／ｄｎが限りなくゼロに近づいていきます。このときのΔＫを下限界応力拡大係数範囲Δｋ_ｔｈと言います。

よってＰと比例関係にあるΔＫが，ΔＫ＜ΔＫ_ｔｈ　を満足するときｄａ／ｄｎがゼロとなります。

鉄鋼材料の場合ΔＫ_ｔｈは２～３［ＭＰａ√ｍ］です。ΔＫ_ｔｈがゼロではなくある値を持つことから，ｄａ／ｄｎがゼロのとき，つまりき裂が進展しないときの荷重振幅Ｐもゼロではなくある値を持つことになります。以上が破壊力学を使ったＬ金具が疲労破壊しない理由の説明です。

参考文献

１）破壊力学

２）破壊工学の基礎知識

３）泉，酒井，理論と実践がつながる　有限要素法シミュレーション，森北出版，(2010)

４）日本機械学会，機械工学便覧　A4　材料力学，p118，(1984)