仮想仕事の原理
剛性マトリクスを導出するために採用した仮想仕事の原理は以下のようなものです。
「物体がこれに働くいくつかの力の作用の下でつり合い状態にあるとき,この物体に微小な仮想変位を与えても,物体中に新たに蓄えられるエネルギーとその物体に加わるすべての力がなす仕事の総和はゼロである。」
学生のときはこれを暗記しました。しかし「仮想変位」というからにはどんな変位でもよいわけで,こんな変位を与えても物体中に発生する内部仕事(仮想変位によって生じるひずみと応力との積)と外力による外部仕事(外力と仮想変位量の積)の和がゼロだなんていわれても,どこの馬の骨だかわからない変位を導入してこれが本当に成立するかなんてピンときませんね。というわけで仮想仕事の原理を導出します。
釣り合い式 (応力の釣り合い式)
仮想仕事の原理は力の釣り合い式と等価(弱形式)と言われています。釣り合い式から出発します。
釣り合い式は次式です。
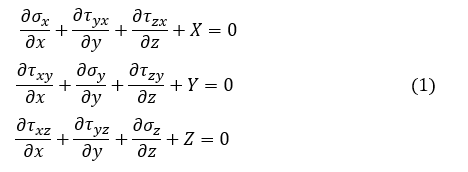
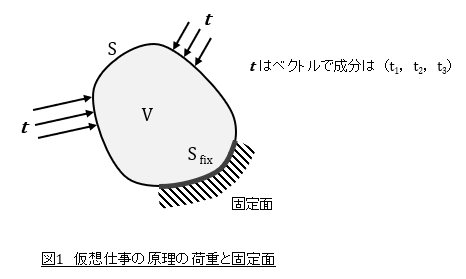
X,Y,Zは,物体に作用する単位体積当たりの力[N/m3]です。重力の場合,Z = -ρg となります。
せん断応力について次式が成立します。
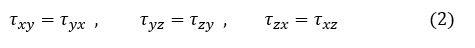
総和規約を使った導出
(1)式を総和規約で表現して導出しましょう。釣り合い式は次式となります。3つの式が一つになりました。総和規約に精通されていない方は総和規約を使わない導出に進んでください。総和規約に精通されている方にとっては,多分このページは不要でしょう。
自由指標 i は,i=1が x ,i=2が y ,i=3が z です。ダミー指標 j は,j=1が x ,j=2が y ,j=3が z です。

表面に作用する外力(表面力ベクトル) ti は次式で表現します。σij は,ti と釣り合って物体内部で発生している応力テンソルでCauchyの応力テンソルと呼ばれています。ni は物体表面の外向き法線ベクトルです。

ti は表面力ベクトル(単位面積当たりの外力の3成分)です。ただしこの式は物体が固定されている表面(図1の Sfix 面で,この面には反力が発生しています)には適用しません。固定されていない表面 S に適用します。外力が作用していない面は ti=0 となります。
任意のベクトル δi を導入します。仮想変位と名付けましょう。(3)式に任意のベクトル δi を掛け算して和とを取って,対象とする領域全体で体積積分しましょう。(3)式はゼロなので積分はゼロになります。
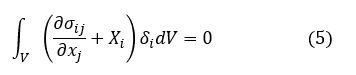
カッコ内第1項を部分積分の式を使って変形します。
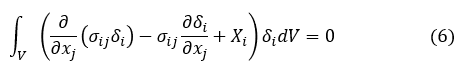
発散定理(総和規約を使わない版で詳しく説明します。)を使って,カッコ内第1項を面積分に変えます。
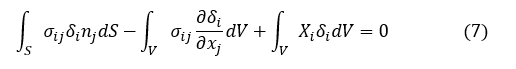
上式第2項を変形します。第2項のベクトル δi の偏微分を対称テンソルと反対称テンソルの和に分解します。第2項の積分内は次式となります。
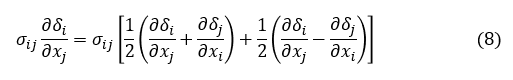
応力テンソル σij は対称テンソルでした。そして上式第2項は反対称テンソルです。対称テンソルと反対称テンソルの積はゼロなので第2項はなくなり,(7)式は次式となります。
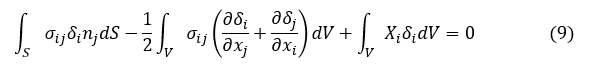
順序を入れ替えて
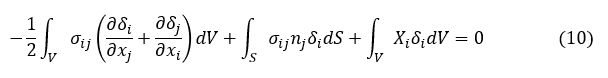
上式第2項に(4)式を代入し,仮想変位によるひずみを δεij と表記します。
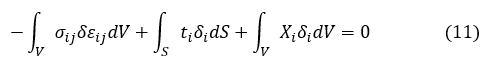
上式第1項は仮想変位によって生じたひずみと応力との積なので内部仕事で,第2項は表面力ベクトルと仮想変位との積なので外部仕事,第3項は外部から作用する体積力に仮想変位を掛けたもので外部仕事です。仮想仕事の原理が導かれました。かなりあっさりしたものですね。今度は総和規約を使わないで導出しましょう。
上式には若干の制約がついて,仮想変位 δi は固定面 S fix 上ではゼロであるとします。
総和規約を使わないで行う仮想仕事の原理の導出
今度は総和規約を使わないで導出します。(10)式の第1項に1/2がついていること,第1項が「応力×ひずみ」になっていること,および発散定理についても詳しく述べていきます,
任意のベクトル δ を導入します。太字 はベクトルを意味します。δ は次式で表現されます。後に δ を仮想変位にしますが,この時点では δ は何でもよいのです。

i,j,k は,X軸,Y軸,Z軸を向く大きさ1のベクトル(単位ベクトル)です。
(1)式は3つの式から構成されるのでベクトルで表現しましょう。ベクトルと言ってもその方向は何も意味を持っていません。ただ3つの量をひとつのベクトル量で表しただけです。
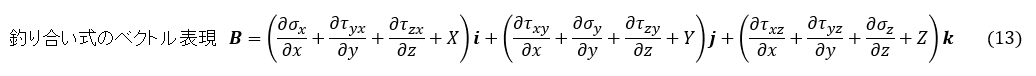
釣り合い式の右辺はゼロなので B の各成分はゼロです。ふたつのベクトルの内積を計算してもゼロ(スカラー量)になりますね。別に δと B が直交しているわけではありません。そして,領域Vについて積分してもゼロですね。次式が成り立ちます。
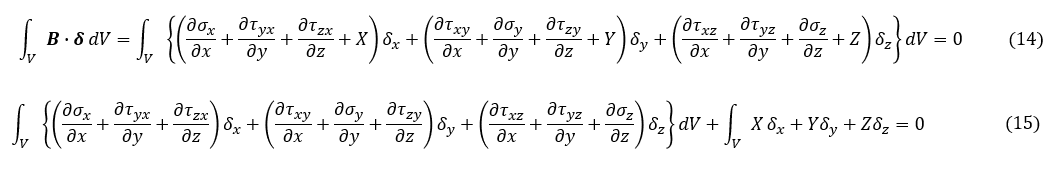
体積力をベクトル X で表現します。 X は次式となります。

(15)式の第2項は,X と δ の内積なので(15)式は次式となります。
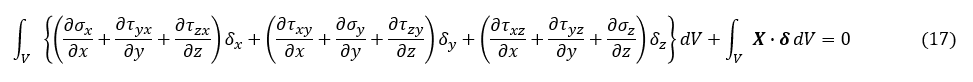
少々面倒ですが,(17)式第一項を展開しましょう
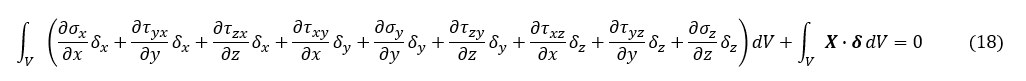
積の微分公式を次式に示します。
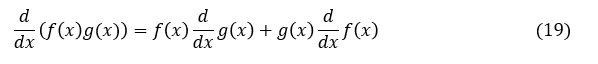
σx や δx は,x,y,z の関数なので,その偏微分は次式で表されます。
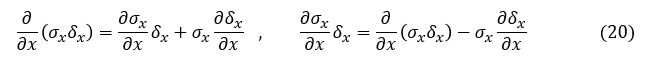
τyz,τzx,...,δy,δz についても同様に積の微分公式を使って変形します。(18)式は次式となります。
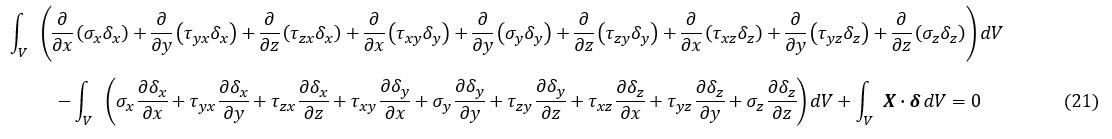
上式第1項を∂/∂x,∂/∂y,∂/∂zでまとめておきます。
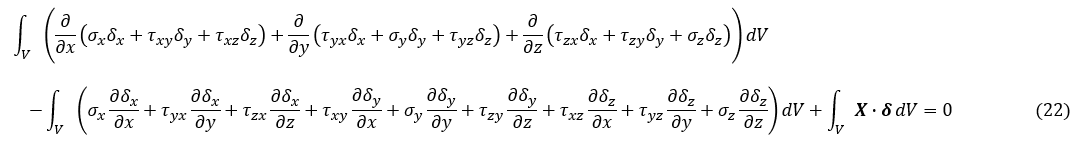
上式第1項を発散定理を使って変形します。発散定理は次式で表されます。Vは領域,Sは領域を囲う閉曲面, n はSの外側を向く大きさ1の法線ベクトルです。

A は任意のベクトル,∇ はハミルトンの演算子と呼ばれ次式で定義されています。
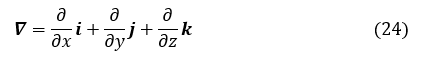
(23)式の両辺はベクトルの内積なので,展開しましょう。
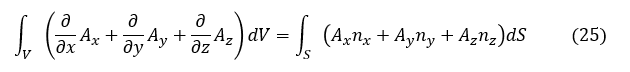
仮想仕事の原理の式(22)式第1項は(25)式の左辺の形をしています。Ax,Ay,Az は以下になります。
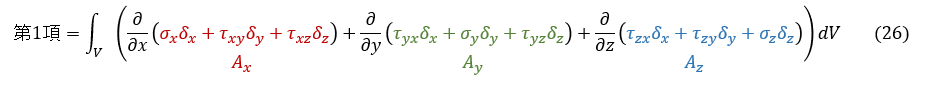
発散定理を適用すると,(22)式第1項は以下となります。体積積分が面積分に変わります。
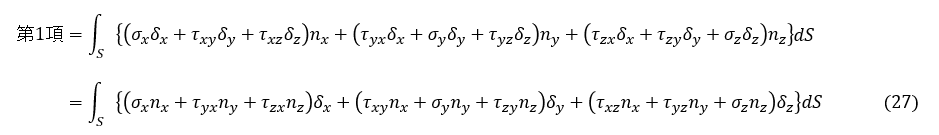
上式はベクトルの内積の式になりますので,以下にように変形します。
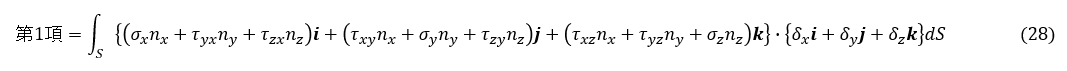
表面に作用する外力(表面力ベクトル )t と物体内部に発生している応力の関係を調べます。図2に示すように,物体の表面の微小な領域を切り取ります。dSは物体表面でdS面に表面力ベクトル t が作用しています。一方物体内部には,赤,緑,青ベクトルで表した応力が発生しています。表面力ベクトルと応力が釣り合っています。Y方向の力の釣り合いを考えましょう。
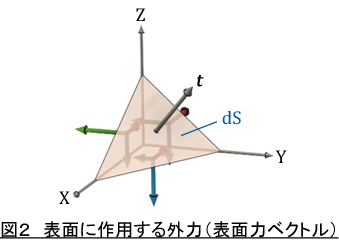
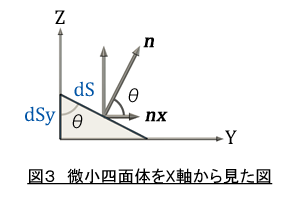
その前に,X軸に垂直な面dSx,Y軸に垂直な面 dSy ,Z軸に垂直な面 dSz と dS の関係を調べましょう。図3は微小な四面体をX軸から見た図です,ベクトル n はdS面の法線ベクトルで大きさを1とします。
微小四面体のY軸に垂直な面 dSy の面積は dScosθ ですね。また表面の法線ベクトルのY方向成分 ny は,|n| cosθなのですが,|n| =1 なので,ny =cosθです。よって,dSy の面積はdSny となります。(29)式です。
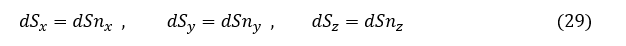
Y方向の力の釣り合いを考えましょう。表面力ベクトル t の Y方向成分 ty は物性内部の応力と釣り合っているので次式が成立します。
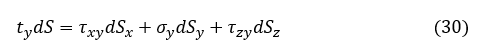
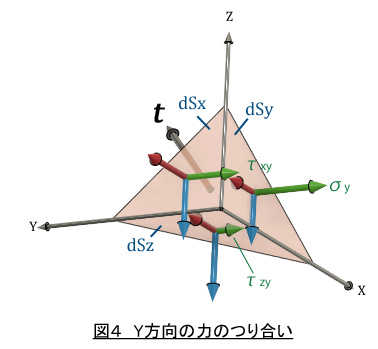
(30)式に(29)式を導入します。
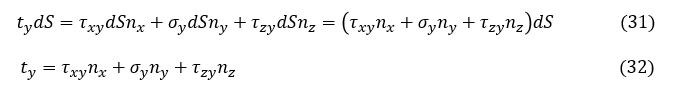
同様にして以下の3式が成立します。
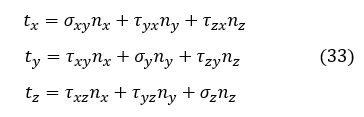
仮想仕事の原理の式(22)式の第1項は,以下のように表面力ベクトル t によって表すことができるようになりました。
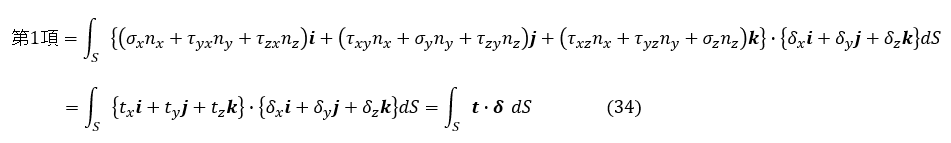
仮想仕事の原理の式第1項が片付きました。第2項を変形していきましょう。行列の内積を記号「:」で定義します。この内積は単に式を見やすくするためだけに使います。
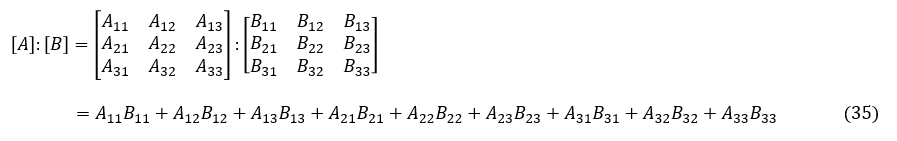
仮想仕事の原理の式第2項は,「:」を使うことで行列で表現できます。
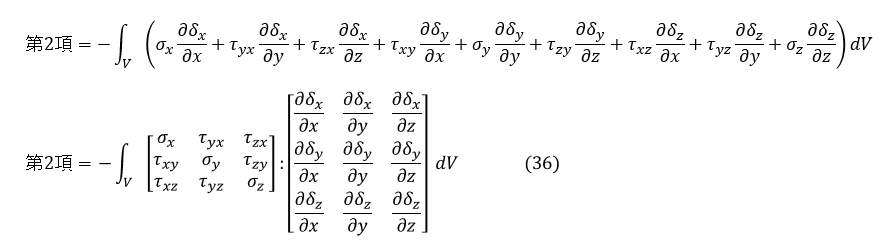
任意の行列は対称行列と反対称行列の和に分解できます。(36)式の二つ目の行列をまず半分にして,同じものを足したあと差引いても値は変わらないので,次のように変形します。

反対称行列とは,ある要素に対しその要素の行と列を入れ替えた要素は絶対値が同じで符号が反転している行列です。対角項は Aii = -Aii とならないといけないので,これを満足する数はゼロです。よってい対角項はゼロです。上式第1項は対称行列,上式第2項は反対称行列です。
応力を表す行列(応力テンソルと呼びます)は,(2)式を用いると次のように対称行列になります。
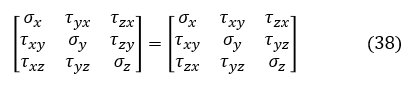
対称行列と反対称行列の内積はゼロなのですが,(37)式第2項を計算しましょう。
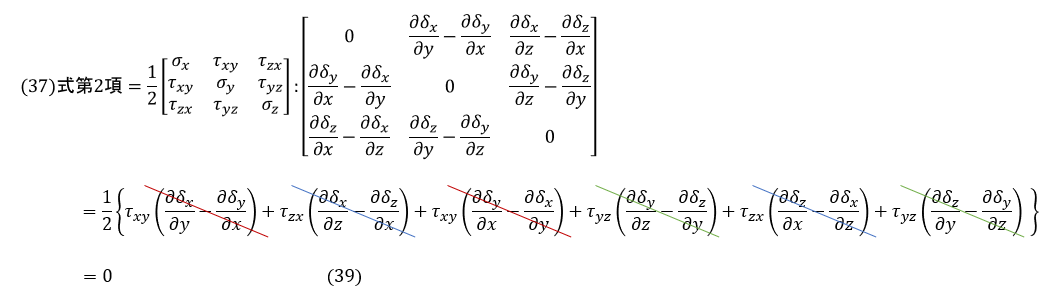
仮想仕事の原理の式第2項は次式となります。
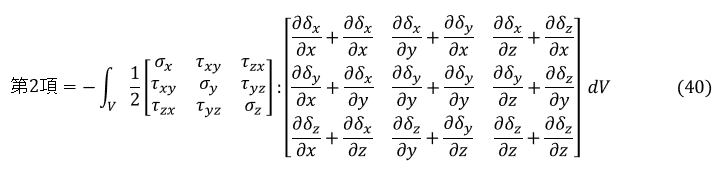
今まで δ は任意のベクトルでした。ここで δ を仮想変位と呼んで変位に関する量としましょう。そして,仮想変位は図1における固定面 Sfix でゼロベクトルであるとします。
変位の偏微分はひずみでした。しかしこのひずみは仮想変位 δ によるひずみなので,εx ではなく δεx と表記することにします。仮想変位によるひずみは次式となりますね。
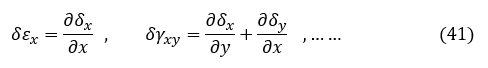
仮想仕事の原理の式第2項をひずみで表します。
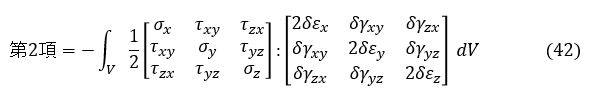
式を展開しましょう。
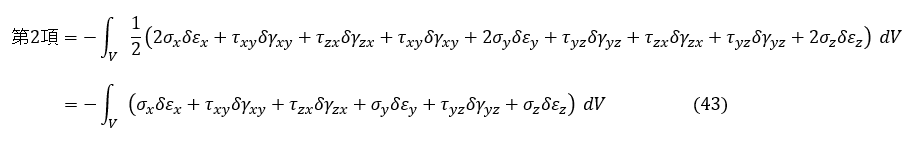
これで第2項も片付きました。(21)式に(34)式と(43)式を代入しましょう。
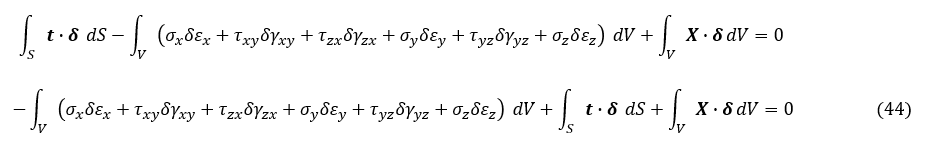
応力とひずみの積はひずみエネルギで仮想変位によって物体中に新たに蓄えられるエネルギーです。力と変位 δ の積は力がなす仕事です。よって,(44)式第1項は「物体に微小な仮想変位を与えたことによる物体中に新たに蓄えられるエネルギー」で,第2項は「物体表面に作用する外力がなす仕事」で,第3項は「重力など体積力がなす仕事」となり,これらの総和がゼロとなります。
仮想仕事の原理を表す式ができ上がりました。
仮想変位の原理の解釈
以上のように,仮想仕事の原理を表す式は釣り合い式を何の法則も使わずにただ数学的な式の変形で導くことができました。かつて仮想仕事の原理を暗記していた私は,ダランベールには悪いのですが次のように解釈することにしました。
「仮想仕事の原理の式は釣り合い式を数学的に操作で導くことができ,その式を日本語に翻訳したものが仮想仕事の原理である。」
仮想変位の原理の式の2次元版
要素剛性マトリクスの導出のページの(31)式と(44)式が見た目が異なるので(44)式を変形します。仮想変位 δ を次式に書き換えます。

表面力ベクトル t も次式に書き換えます。

物体力ベクトルも次式に書き換えます。

平面応力問題を対象としているため,(44)式第1項のZ方向成分を含む応力をすべてゼロにします。そして,(45)式,(46)式,(47)式を(44)式に代入します。
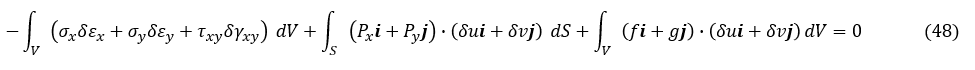
二次元問題なので板厚をhとすれば dV=hdxdy となり体積積分は面積積分に変わります。上式第2項の微小面dSは微小線素dsに変わり面積分は線積分に変わります。積分記号も書き換えます。そしてベクトルの内積を展開します。
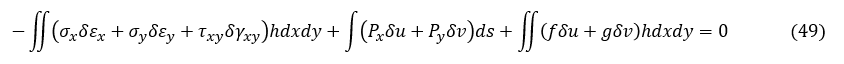
順序を入れ替えると要素剛性マトリクスの導出のページの(31)式になりました。
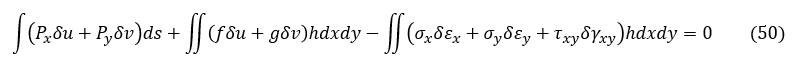
Information
仮想仕事の原理 を追加しました。


