低減積分要素と完全積分要素

ＨＯＭＥ　＞　ＣＡＥ・有限要素法　＞　低減積分要素と完全積分要素

要素剛性マトリクス[k]を求めるときにはガウス・ルジャンドルの数値積分公式を使って数値積分をします。次式です。[B]は変位－ひずみマトリクス，[D]は応力－ひずみマトリクス，[J]は座標変換によるヤコビアンです。ガウス・ルジャンドルの数値積分公式では計算点数の違いにより，n=1，2，3，4，・・・と選択肢がいろいろあります。2n-1次の多項式は厳密な積分が計算できます。例えば，2次の多項式 f(ξ)=aξ²+bξ+C の場合，n=2（2n-1=3）で厳密な積分ができます。

四角形１次要素の場合

上記積分では積分点の計算を行いますが，積分点の取り方は任意で例えば図2のような積分点とすることができます。

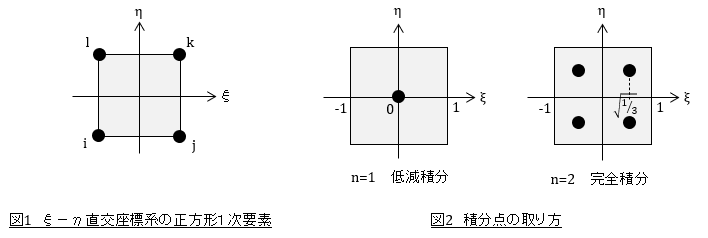
積分点を1点（n=1）とした場合を低減積分要素，4点（n=2）とした場合を完全積分要素といいます。[B]^T[D][B]det[J]₁₁は，有限要素法の定式化のページで導出したように以下の形をしており，分子だけに注目すればξ，ηの2次式なのでn=2で厳密な定積分ができるのですが，分母がξ，ηの1次なのでnをいくらにしても厳密な定積分を行えるわけではありません。しかしn=2の場合を完全積分と言っています。「完全」とは少し言いすぎですね。

はりの曲げ問題のように曲げ応力が発生する場合，完全積分要素を使うとロッキングといってかなり剛性が高めの計算結果となります。実務では使えません。この問題を回避するために低減積分要素が開発されました。低減積分要素では剛性が低めの計算結果となります。しかしアワーグラスモードと言って，とんでもない変形形状の計算結果となることがあります。アワーグラスモードは要素分割を細かくすることで回避できます。

商用有限要素法ソフトではいろいろな創意工夫がなされていて，ロッキングとアワーグラスモードが出にくい要素が実装されていますが，その詳細は公開されていません。

四角形２次要素の場合

２次要素では積分点は図3のようになります。

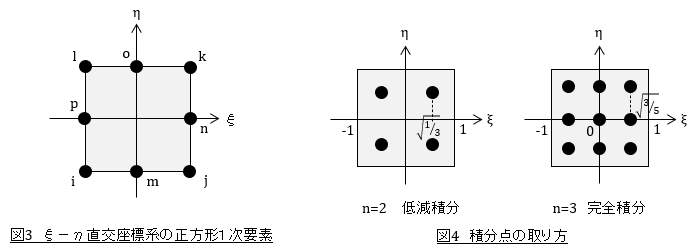
積分点を4点（n=2）とした場合を低減積分要素，9点（n=9）とした場合を完全積分要素といいます。[B]^T[D][B]det[J]_ijの分子だけに注目すればξ，ηの4次式なので厳密な定積分のためにはn=3（2n-1=2*3-1=5）で十分なのですが，分母がηの2次式なので厳密な積分できていません。しかし，n=3で完全積分と言われています。

２次要素ではロッキングもアワーグラスモードも発生しません。私の経験から言うと年に1度くらいアワーグラスモードに遭遇しますが，要素分割をやり直すことで回避しています。また完全積分要素が選択されることは少なく，商用有限要素法ソフトのディフォルトは低減積分要素となっているようです。

詳しくは有限要素法の定式化のページを参照してください。