時刻歴応答解析

ＨＯＭＥ　＞　ＣＡＥ・有限要素法　＞　時刻歴応答解析

構造物に外力や強制変位が加わったときの，構造物の過渡的な変形，応力，ひずみを求める解析が時刻歴応答解析です。図１に示すような１軸テーブルにコラムを介してヘッドが固定されている機械について，１軸テーブルが移動したときの全体の変形を求めてみましょう。

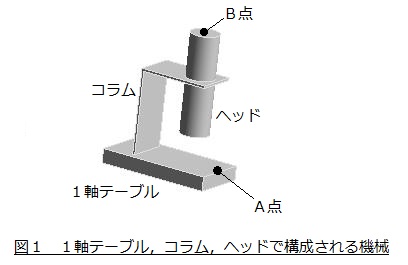
１軸テーブルをゆっくり移動させたときは，ヘッドとコラムは１軸テーブルの動きと同じ動きをしますが，１軸テーブルを早く移動させたときは，慣性力が働くためコラムが変形しヘッドとコラムは振動します。時刻歴応答解析結果を図２に示します。ヘッドとコラムが振動している様子がわかります。

　　　　図２　時刻歴応答解析例

Ａ点とＢ点の変位の時間変化を図３に示します。Ａ点の変位（図の青い線）は１軸テーブルの動きとなります。Ｂ点の変位はヘッドの過渡的な振動変位となります。

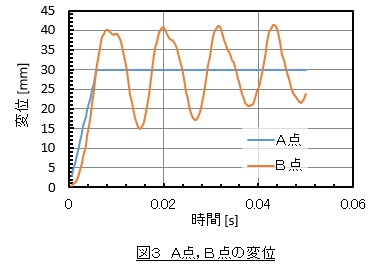
モーダル解析では振動形状はわかりましたが変位の絶対値はわかりませんでした。周波数応答解析ではsin波状に加振したときの定常状態の振幅はわかりましたが，過渡的な応答はわかりませんでした。時刻歴応答解析によって過渡的な応答を求めることができます。一方，時刻歴応答解析で定常状態の応答も求めることはできますが，計算時間がとても長くなって現実的ではありません。

図２，図３では変位を述べましたが，時刻歴応答解析では変位の他に応力やひずみなど静解析で求まるすべての量を計算することができます。

モード重ね合せ法とフル法

有限要素法ソフトで時刻歴応答解析をするときにモード重ね合せ法で計算するかフル法で計算するか選択する必要があります。モード重ね合せ法は事前にモーダル解析を実施してその結果得られるモーダルパラメータを使って計算します。計算時間が圧倒的に短いのが特徴ですが，現象を十分再現できるだけの振動モードを求めなければならないことに注意が必要です。また線形解析に限定されます。フル法はモーダル解析を行わず直接計算する方法です。フル法では非線形解析（摩擦あり接触問題，弾塑性変形，大変形問題）も可能となります。

時間刻み幅Δｔについて

時刻歴応答解析では時間刻み幅Δｔを設定する必要があります。注目したい振動の周期をＴとすれば，ΔｔはＴ／２０程度にする必要があります。上の例では，Ｔ＝0.012[s]，Δｔ＝0.00059[s]としました。

上の例では計算終了時刻を0.071[s]として計算しました。0.071[s]をΔｔで割ると120です。つまり，マトリクス計算を120回繰り返したことになります。計算時間は線形静解析の約120倍かかったことになります。また結果ファイルも120倍の容量になりました。計算時間と結果ファイル量が劇的に増えるため，計算終了時刻とΔｔの選定には注意が必要です。