剛体変位

ＨＯＭＥ　＞　ＣＡＥ・有限要素法　＞　剛体変位

変位拘束境界条件の記号の説明

剛体変位の説明の前に変位拘束境界条件の記号の説明をします。

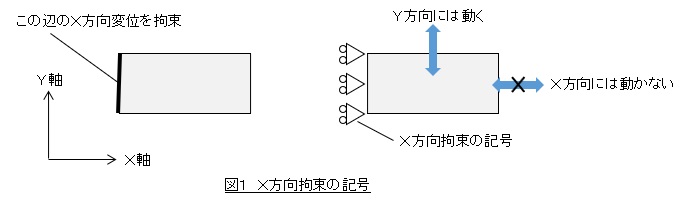
Ｘ方向拘束の記号を図１に示します。三角形と二つの丸で表現します。丸がコロであると解釈して。転がっていると考えればよいと思います。

剛体変位の例１

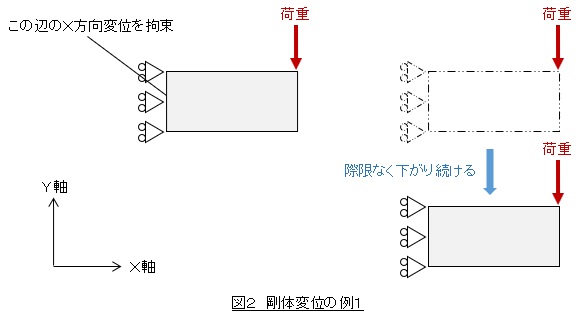
図２は，長方形の左側の辺のＸ方向変位を拘束し右上に－Ｙ方向の荷重を加えた場合です。長方形は際限なく下がり続けますね。これが剛体変位の例です。有限要素法ソフトは，「Ｙ方向の変位が許容値を超えました。」とか「ピボットが非常に小さくなりました。」などのエラーメッセージを出力して異常終了したり，変位がべらぼうに大きな値として計算結果を出力したりします。

有限要素法ソフトの中ではどうなっているのでしょうか。有限要素法詳細では，有限要素法は連立方程式を解いていると説明しました。連立方程式を解くには，方程式の数と未知数の数が一致していなければなりません。しかし剛体変位が生じる場合，未知数の数より連立方程式の数が少ないのです。よって，解を得ることができないのです。

剛体変位の例２

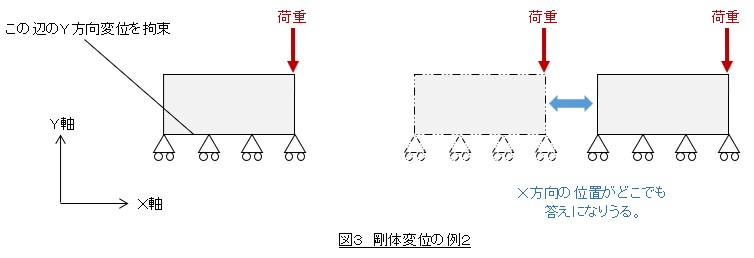
図３は長方形の下辺のＹ方向変位を拘束した場合です。今度はＹ方向に際限なく動くことはありません。しかし，長方形がＸ方向にどれだけ移動していても答えになりえるので，これも剛体変位となります。

剛体変位の例３

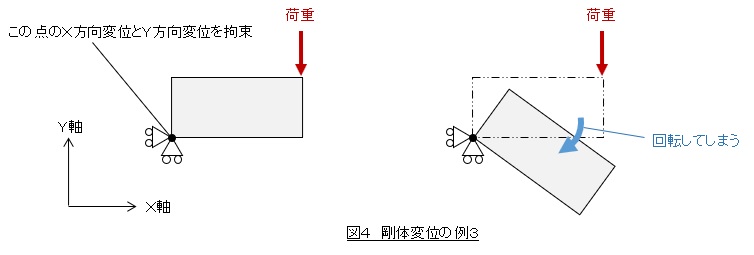
図４は長方形の左下の点のＸ方向変位とＹ方向変位を拘束した場合です。今度はＸ方向にもＹ方向にも動くことはありません。しかし，長方形が左下の点を中心として回転してしまい，これも剛体変位となります。

剛体変位の防止

以上のように剛体変位が発生すると，有限要素法で変位や応力を求めることはできません。上述した例は二次元問題で説明したので，運動の自由度は，①Ｘ方向並進，②Ｙ方向並進，③ＸＹ平面内の回転で，剛体変位を避けるためにはこれら３つの運動を拘束しなければなりません。解析の前に頭の中で①②③を思い浮かべて剛体変位がしないことを確認してください。

三次元問題での運動の自由度は，①Ｘ方向並進，②Ｙ方向並進，③Ｚ方向並進，④Ｘ軸周りの回転，⑤Ｙ軸周りの回転，⑥Ｚ軸周りの回転です。計算の前にこれら６つの運動をしないことを頭の中で確認してみてください。私の経験では，有限要素法ソフトによっては剛体変位が生じていてももっともらしい答えを出力するものがありました。しかしこの答えを信用することはできません。剛体変位が生じていないか確認する習慣をつけましょう。