応力特異点

ＨＯＭＥ　＞　ＣＡＥ・有限要素法　＞　応力特異点

応力特異点とは

弾性解析をしていると，応力集中が激しいところのごく小さな領域（１節点だけ）で極端に大きな応力が発生することがあります。これは応力集中の結果ですので，要素分割を細かくしていくと最大応力値がある一定値に収束してほしいのですが，要素分割を細かくすればするほど最大応力値も大きくなってしまう現象によく遭遇します。このような点を応力特異点と言います。①コーナＲがゼロで形状が変化するところ，②節点やソリッドモデルの点（キーポイント）に荷重をかけた場所や辺（ライン）に荷重をかけた場所，③拘束した点，辺，面の近傍　に，発生します。

図１に示す応力分布図のレジェンドの最大値だけを見ていると，応力特異点の応力値を見て，それと許容応力とを比較してしまう結果となる場合がありますので注意が必要です。

上記①②③について説明していきます。

①コーナＲがゼロで形状が変化するところで発生する応力特異点

図２に示すような段付き板に引張り荷重Ｐが作用している場合を例にとります。段の部分には曲率半径ρのコーナＲがあるとします。最大応力σｍａｘはＡ点近傍で発生します。応力集中係数は図３のようになります。

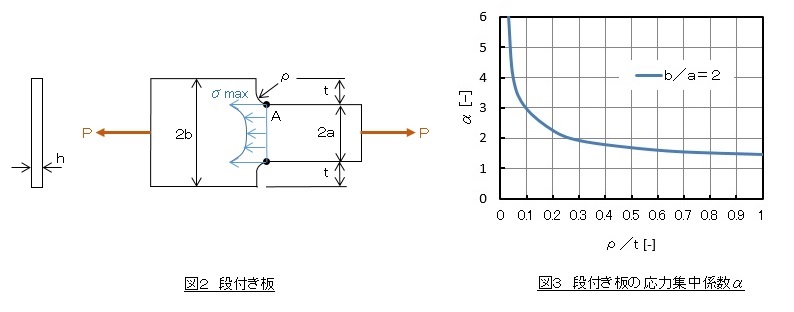
今，曲率半径ρがゼロの場合を考えます。図３から応力集中係数αが無限大になるのでＡ点の応力は無限大になります。では，曲率半径ρがゼロの場合を有限要素法で計算したらどうなるのでしょうか。この結果を図４に示します。

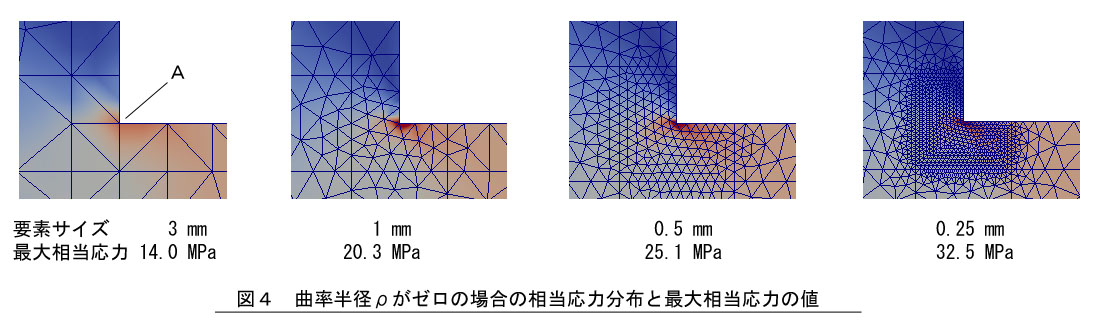
要素サイズを細かくすればするほど最大相当応力が大きくなる結果となりました。Ａ点の応力は弾性力学的には無限大です。一方，有限要素法では，要素分割を細かくするほどその計算結果が弾性力学の解に近づきます。今回の場合，要素分割を細かくするほど計算結果が無限大に近づこうとします。これでは，いくら要素分割を細かくしてもＡ点の応力は収束しませんね。この現象が曲率半径がゼロの部分の応力特異点発生のメカニズムです。

それでは，曲率半径ρが３[mm]の場合を計算してみましょう。結果は図５のようになりました。最大相当応力は17.3[MPa]に収束しました。

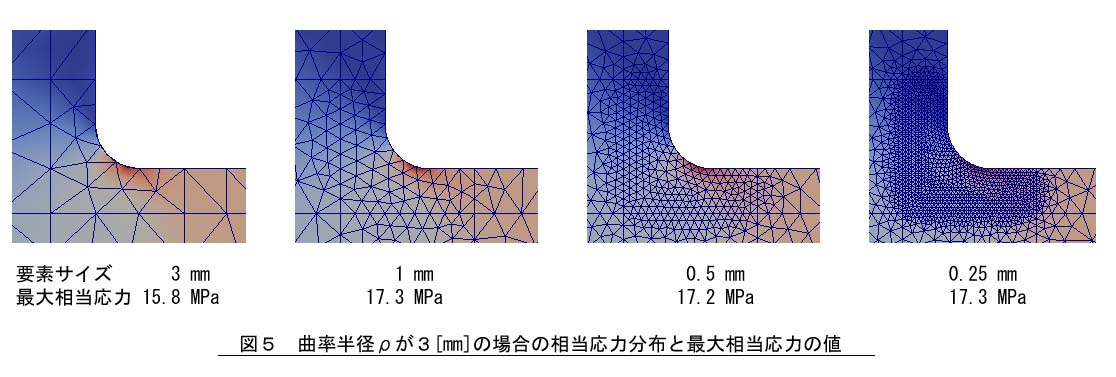
10[mm]あたりの要素分割数と最大相当応力の関係を図６に示します。曲率半径をゼロとした場合は要素分割数を増やしても応力値が収束しませんが，曲率半径を３[mm]とした場合は応力値は一定値に収束します。このように応力特異点の回避方法はコーナ部の曲率半径をとることです。

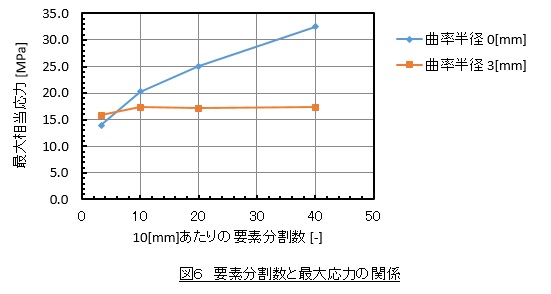
設計において疲労破壊を防止するために十分に大きなコーナＲをとることは基本ですが，小さなコーナＲの設計をせざるを得ないことがあります。このような場合に応力値が収束するような要素分割をすると，要素数が多くなりすぎてしまい計算ができない場合があります。例えば，すみ肉溶接の溶接ビード止端部などです。このような場合，無理してコーナＲをとる必要はありません。切欠係数βを導入して疲労破壊の有無を予測する方法があります。ホットスポット応力を求めて，ホットスポット応力を公称応力の代用として公称応力ベースの疲労評価をします。

②点や辺に荷重をかけたところで発生する応力特異点

図７と図８に点と辺に荷重をかけた場合の変形と相当応力分布を示します。

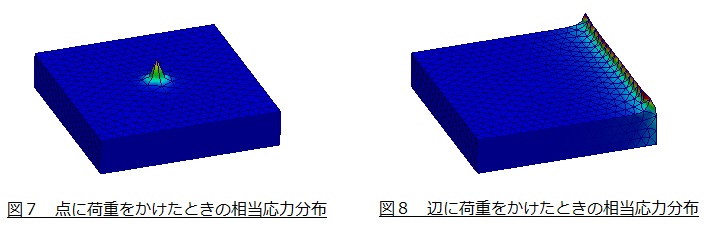
荷重をかけたことろで大きな応力と変位が発生しています。応力は　荷重÷面積　ですね。一方，点や辺の面積はゼロです。よって荷重点の応力は　荷重÷ゼロ　となって無限に大きな応力となってしまいます。この結果，点荷重や辺荷重をかけた点や辺は応力特異点となってしまいます。対策としては，荷重を面にかけることになります。

③拘束した点，辺，面の近傍で発生する応力特異点

点や辺を拘束した場合は，上記②と同じ理由から拘束の反力によって発生する応力が無限大になって応力特異点になることは理解できますね。しかし，面を拘束した場合も応力値が高くなってしまいます。

図９のような片持ちはりを例にとって計算してみましょう。Ａ点のｘ方向応力は，はり理論から300[MPa]です。Ａ点の第一主応力も300[MPa]です。図１０は第一主応力の計算結果です。図のＡ部の最大応力は428[MPa]となってしまいました。図のＡ部の最大応力は要素分割を細かくしていくとだんだん大きくなり，これも応力特異点となります。

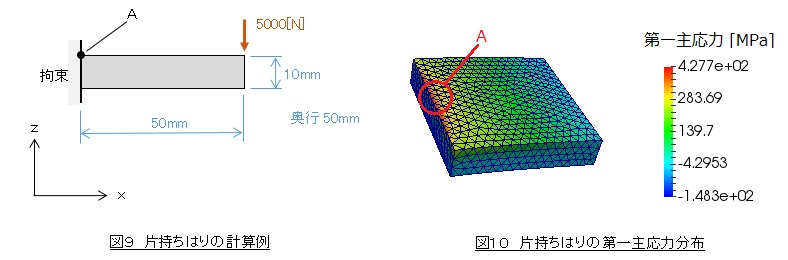
応力特異点となる理由は，拘束面上の節点のｘ，ｙ，ｚ変位を拘束しており，過剰拘束となっているためです。対策としては，過剰拘束をなくすことが考えられますが，これがなかなか面倒な作業となります。拘束面の応力値を読取るのではなく，例えばひとつとなりの節点の応力など近傍の応力を読取る対処が現実的です。

以上が，応力特異点の種類とその対処法です。