アイソパラメトリック要素

ＨＯＭＥ　＞　ＣＡＥ・有限要素法　＞　アイソパラメトリック要素

荷重が作用している任意形状の物体内の変位分布u，vは座標x，yの関数ですが，弾性力学の方程式を解いてその関数式を直接求めることはほぼ不可能と言っていいでしょう。有限要素法では任意形状を小さな要素に分解して，要素内の変位を次式のように座標の１次式ないしは２次式で近似し，任意形状の物体内の変位分布は各要素の変位分布の集合とします。

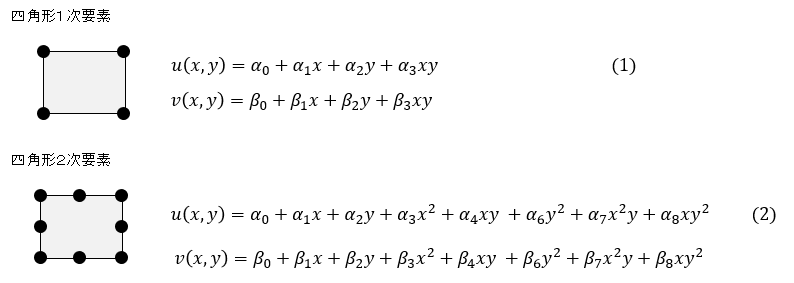
しかし，この方法で係数α_i，β_iを求めることはかなり難しいです。ここで工夫して別の直交座標系ξ，ηを導入して，図1のような正方形要素を考えます。

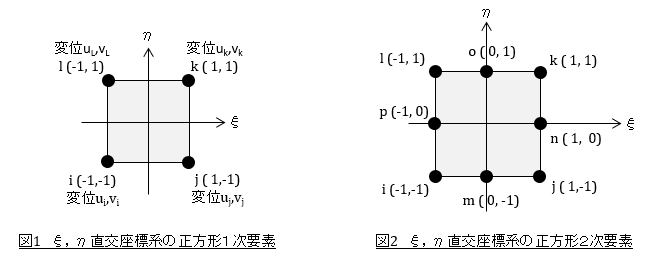
i節点の変位をu_i，v_i，j節点の変位をu_j，v_jなどとすれば，要素内の任意の位置の変位は次式で表すことができます。

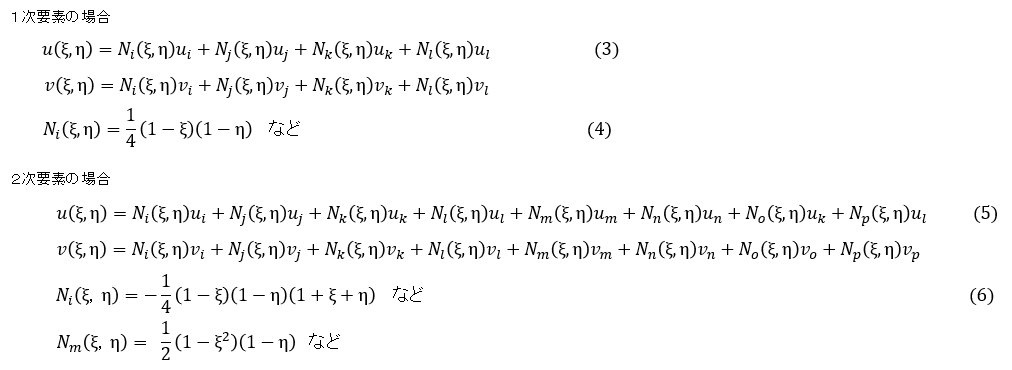
変位u，vが座標ξ，ηの１次式ないしは２次式で表されました。N_i（ξ，η）などを形状関数といいます。

実際の要素は図３左図のように任意の形状をしています。これを正方形要素に変換する必要があるから，x，yとξ，ηの関係式を用意する必要があります。座標変換ですね。次式です。

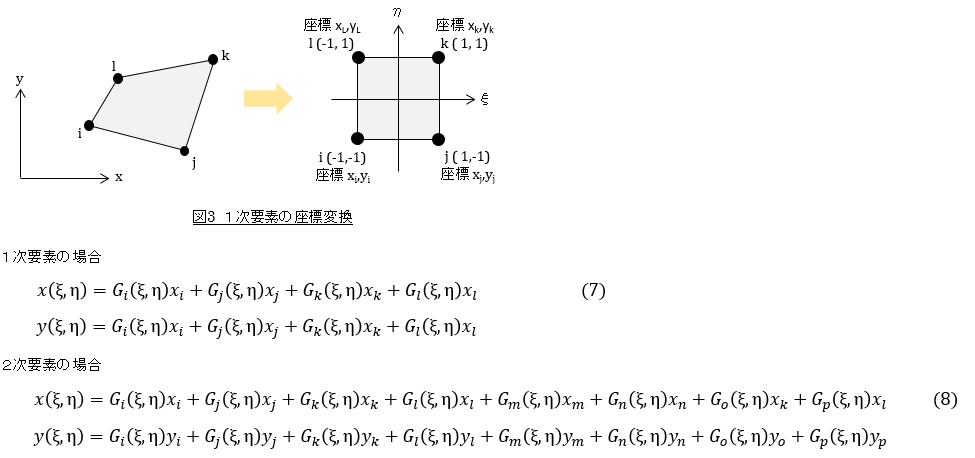
N_i（ξ，η）とG（ξ，η）_iは要求される振る舞いが同じであるので，同じ形にできます。N（ξ，η）とG（ξ，η）を同じ形にして，つまり変位を表す形状関数と，座標変換のための形状関数を同じ形にして要素剛性マトリクスを導きます。このようにして作られた要素をアイソパラメトリック要素といいます。アイソ（iso）は「同じ」という意味です。

詳しくは有限要素法の定式化のページを参照してください。