対称問題

ＨＯＭＥ　＞　ＣＡＥ・有限要素法　＞　非線形解析

非線形解析

非線形解析を分類すると以下のようになります。ひとつづつ説明していきます。

• 材料非線形問題
  　　弾塑性材料を扱う問題
  　　超弾性材料を扱う問題
  　　クリープ変形を扱う問題

• 大変形問題

• 接触問題

材料非線形問題　弾塑性解析

塑性変形を考慮する問題は弾塑性解析を行います。このためには，塑性変形部分を含めた応力－ひずみ線図が必要になります。応力－ひずみ線図は，多直線で近似する場合（図１）と２直線で近似する場合（図２）に分けられます。多直線で近似する場合は実際に引張試験をする必要があり手間がかかります。２直線で近似する場合，必要とする材料定数は，ヤング率，ポアソン比，降伏応力，接線係数だけで済み，割と手軽に解析できます。

接線係数を説明しておきます。図２において弾性領域での傾きがヤング率で，塑性領域の傾きが接線係数です。接線係数の単位は[Pa]です。降伏応力は割と簡単に調べることができますが，接線係数はなかなか文献に載っていません。鉄鋼材料の場合1.45 x 10⁹[Pa]，アルミニウム合金の場合5.00 x 10⁸[Pa]，銅合金の場合1.15 x 10⁹[Pa]程度でしょう。

金属材料は加工硬化するので，正確な解析のためには引張試験片の加工硬化の度合いと実際の部品の加工硬化の度合いを一致させる必要があります。しかしこれは至難の技です。加工硬化の度合いが一致していないのがほとんどの場合なので，弾塑性解析結果の塑性変形部分の応力値はおおよその値と考えるべきでしょう。

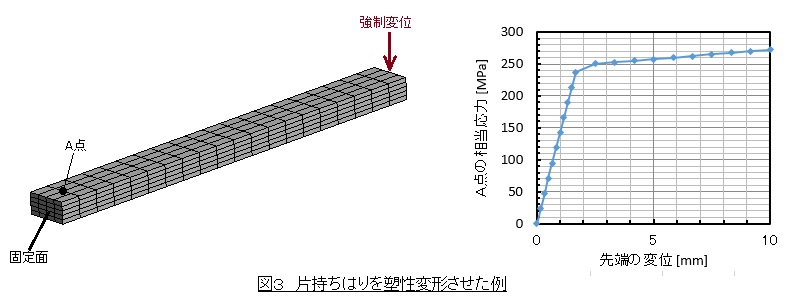
鉄鋼材料でできた片持ちはりを塑性変形させた例を図３に示します。２直線近似で応力－ひずみ曲線を近似しています。図３右図に示すようにＡ点の相当応力とはりの先端変位の関係は，降伏応力である250[MPa]を境にその傾きが変わっており，250[MPa]以下の領域が弾性変形，250[MPa]以上の領域が塑性変形です。

材料非線形問題　超弾性解析

ゴムのように非常に大きな弾性変形を示す材料（超弾性材料）を扱うときは，超弾性解析を行います。変形の前後で体積が変化しない性質を持つことが多く，その応力－ひずみ曲線は非線形であります。材質を定義する物性値が多く，それらを測定するには特殊な測定器が必要です。私はやったことがありません。

材料非線形問題　クリープ解析

ある荷重を加えたときに変形量（ひずみ）が時間の経過とともに増加する現象をクリープ現象と言い，ある一定の変形（ひずみ）を加えたときに応力が時間の経過とともに減少する現象を応力緩和現象といいます。

有限要素法ソフトでクリープ現象を扱うときは，クリープひずみ（ε_cr），ないしはクリープひずみ速度（dε_cr／dt）を次式のような関数で表現します。

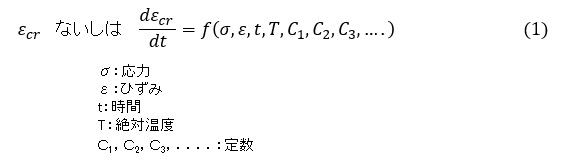
そして，関数の形を指定し，関数の定数Ｃ₁，Ｃ₂，Ｃ₃，．．．を有限要素法ソフトに入力することで解析します。

このためには，数週間か数か月かかるクリープ試験が必要なことはもちろんですが，関数の形を選択して定数を決める作業（これをカーブフットと言います）が必要です。このカーブフィットですが，あっちをフィットしたら，こっちがフィットしないことが起こり，なかなか難しい作業です。

大変形問題

解析対象が目に見える程度の変形をする場合や回転する場合，大変形問題として解析します。具体的には大変形スイッチをＯＮにします。通常の解析は微小変形問題で，力のつり合いは変形前の形状で成立します。大変形問題では，力のつり合いは変形後の形状で成立します。

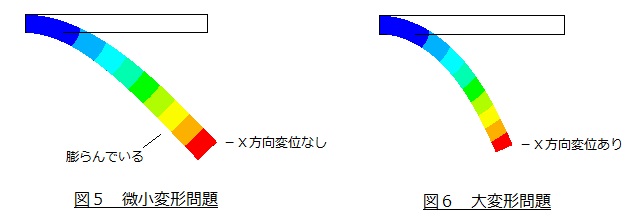
図４に示す先端に荷重が作用するはりの変形で微小変形問題と大変形問題を比較しましょう。Ａ点は－Ｙ方向に変位するのは当然ですが，はりは引き伸ばされているわけではないので－Ｘ方向にも変位します。

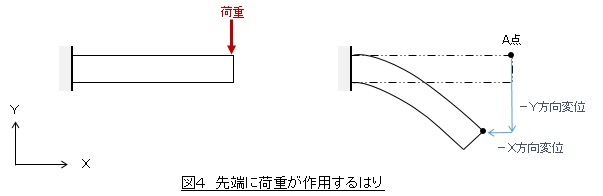
図５に微小変形問題として解いた変位図（有限要素法ソフトの通常の解）を示します。Ａ点の－Ｘ方向変位がありませんし，はりの先端が膨らんでいて体積が膨張していることがわかります。図６に大変形問題として解いた変位図を示します。Ａ点の－Ｘ方向変位があり，体積膨張もありません。

変形量が大きい極端な例を示しましたが，大変形問題として解いたらより正確な結果となります。しかし，通常の変形量は数十倍に拡大しないと見えないような微小な量なので微小変形問題として差し支えありません。

接触問題

接触問題のうち「摩擦あり接触」を選択した場合，非線形問題となります。接触問題では接触要素と呼ばれる表面要素を物体の表面に貼り付けます。図７のような問題を解いてみましょう。はりの先端近傍に座があって，はりの先端と座の間に隙間があります。そしてはりの中央を下方向に強制変位します。はりはたわみますが先端は座に接触して接触後はそれ以上たわまないはずです。

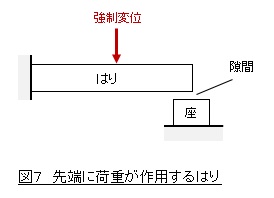
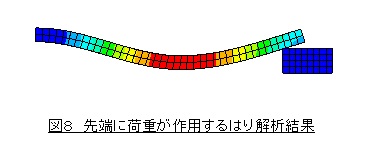
図８に解析結果（変位図）を示します。予想したとおりとなりました。このように接触要素は複数の部品から構成されるアセンブリを扱う場合に重宝します。

非線形問題を解く手順

いきなり本番の非線形問題を解こうとしても，なかなか答えが求まらないことがよくあります。後述する収束しないという問題です。私は以下のような手順で非線形問題を解いています。

　①答えのわかっている単純な問題を非線形問題として解いてみて，有限要素法ソフトの動作確認をする。

　②問題を線形問題として解いてみて，現実的な解になることを確認する。

　③とても粗い要素分割で非線形問題として解いてみる。

　④本番の解析をする。

①②③の手順が無駄だとか工数がかかるとかお思いでしょうが，非線形問題をたくさん取組んだらこの手順の大切さがわかってくるはずです。急がば回れです。

解の収束

線形問題では答えを得るのに剛性マトリクスの逆マトリクスを１回解くだけでよいのですが，非線形問題ではニュートン・ラプソン法と呼ばれる繰返し計算を行います。１回前の計算結果と今回の計算結果の差が許容される範囲内に収まると，答えが求まります。この状態を「収束した」と言います。数十回の繰返し計算をしますので計算時間も数十倍となります。

それで済めばよいのですが，なかなか収束せずに，有限要素法ソフトが答えを求めることをあきらめることがよくあります。異常終了ですね。非線形問題ではソフトベンダーのサポートも有料になることが多いので，収束しないときはとても困ります。収束させるテクニックもあるのですが，それより問題を簡素化することをおすすめします。どんどん簡素化していったら，いつか収束します。そのときどこを変えたか（簡素化したか）に注目します。そこに収束しない原因のヒントがあります。