有限要素法詳細

ＨＯＭＥ　＞　ＣＡＥ・有限要素法　＞　有限要素法詳細

はじめに

有限要素法（finite element method）は，偏微分方程式の近似解を数値的に解く方法のひとつで，構造，伝熱，流体，電磁場などの解析に使用されています。ここでは，弾性体に外力が作用して変形している状態の変位と応力を求める構造分野の有限要素法を説明します。問題を解く段階で変位を未知数としますので，変位法と呼ばれる方法です。

任意の形状の弾性体の変位と応力を，弾性力学の基礎方程式を解いて求めるのはとても難しいことでほぼ不可能と言えます。一方，未知数である変位が多項式などある簡単な式で表現できると仮定して問題を解くことはできます。しかし，弾性体の形状が少しでも複雑となったら，仮定した簡単な式が真の解と程遠いものとなってしまい近似解が求まりません。

そこで問題の対象である弾性体を，要素と呼ばれる小さくてかつ簡単な形状に分割して，要素内では未知数である変位を，座標（ｘ，ｙ）の１次式や２次式など簡単な式で変化すると仮定して変位を求めます。先程「仮定した簡単な式が真の解と程遠いものになる」と述べましたが，小さい要素に分割するとそれぞれの要素内では仮定した簡単な式が真の解の近似式となり得ます。変位の変化が急な場所は要素分割を細かくすることで対処します。小さい要素で得られた変位を統合して，問題の対象である弾性体の変位を求めると，この変位は真の解の近似解となり得ます。また，仮定した簡単な式が適切なものであると，要素分割を無限に細かくするとこの近似解が真の解に近づくことが期待されます。

弾性体のひずみは変位を座標（ｘ，ｙ）で偏微分したものであるため，変位を簡単な式で仮定していることから微分可能なので，ひずみも簡単に求まります。そして応力は，ひずみにヤング率を乗じたものなので求まります。

以上が有限要素法の基本的な考え方です。対象物である弾性体を微小な領域に分割することと，微小な領域の中では未知数である変位を座標（ｘ，ｙ）の簡単な関数として仮定することがポイントです。

それでは，外力が作用する弾性体の変位と応力を有限要素法で求める方法を説明していきます。問題を簡単にするため二次元平面応力問題で話を進めていきます。二次元平面応力問題とは，薄い板に曲げモーメントは作用しなくて二次元的な力だけが作用した状態で，６つの応力成分　σｘ，σｙ，σｚ，τｘｙ，τｙｚ，τｚｘ　のうち，σｚ，τｙｚ，τｚｘ　がゼロの状態をいいます。これを読めば二次元平面応力問題について三角形１次要素を使ってプログラミングができる程度の情報量を記載することを目標とします。

要素分割

図１に示すような弾性体があり，表面の一部が固定されており，異なる表面の一部に外力が作用している問題を考えます。これを図２に示すように小さな領域に分割します。小さな領域を要素（element）といい，要素の頂点を節点（node）と言います。要素と節点で表現される弾性体を有限要素法モデルと言います。図１のような連続体の場合，未知数である変位は座標（ｘ，ｙ）の関数となり，外力と固定は連続体の表面に設定されます。図２のような有限要素法モデルの場合，未知数である変位は各節点毎に設定されその数は有限個となり，外力と固定は節点に対して設定されます。

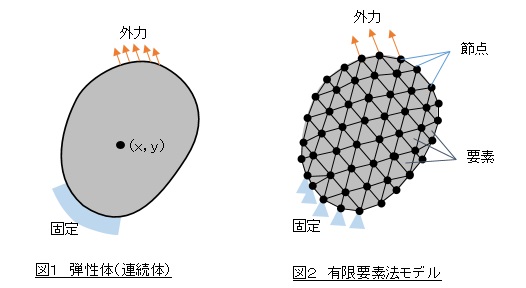
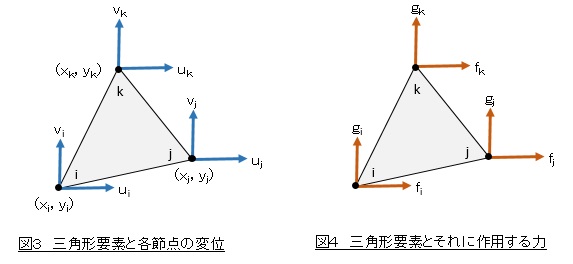
図３，図４は一つの要素を取出したものです。今回説明する要素は三角形１次要素と呼ばれるもので，要素内の変位は(1)式で示されるような座標（ｘ，ｙ）に対して１次式で表されるものです。ひずみは変位を座標で微分したものなので要素内で一定値となり，応力も要素内で一定値となります。

節点には，ｉ，ｊ，ｋと名前を付けます。ｉ，ｊ，ｋの順序は反時計回りとします。各節点の変位を　ｕ_ｉ，ｖ_ｉ，ｕ_ｊ，ｖ_ｊ，ｕ_ｋ，ｖ_ｋ　とし，各節点に作用する力を　ｆ_ｉ，ｇ_ｉ，ｆ_ｊ，ｇ_ｊ，ｆ_ｋ，ｇ_ｋ　と定義します。

図２の有限要素法モデルでは，ある要素とその隣の要素は節点を共有することでつながっています。そして，節点を介して要素に作用する力が授受されると考えます。節点を介して力が授受されると書きましたが，連続体では節点と節点を結んだ線上で力が授受されるので，少し正確でない気がします。しかし，考察を深めていくと結果としてこの考え方でよいとされています。

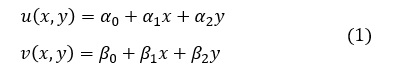
要素剛性マトリクス

節点に力が作用すると要素が変形し節点に変位が生じます。節点に作用する力と節点変位には次式で表される関係があります。(2)式は各成分を表示した形で，(2)’式はマトリクス表示したものです。この式の［ｋ］を要素剛性マトリクスといいます。ばね定数をｋ，ばねの伸びをｕ，ばねに作用している力をｆとすると，ｋｕ＝ｆ　で表されますので，要素剛性マトリクス［ｋ］はばね定数のようなものです。

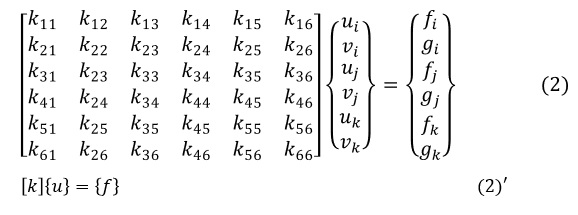
［ｋ］の具体的な値は，材料定数（ヤング率Ｅとポアソン比ν）とｉ，ｊ，ｋ節点の節点座標で決まります。次式となります。

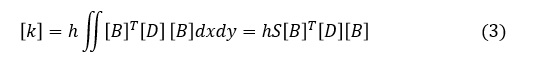
ここで，ｈは三角形要素の板厚，Ｓは面積，［Ｂ］は変位－ひずみマトリクス，［Ｄ］は応力－ひずみマトリクスです。［Ｂ］^Ｔは［Ｂ］マトリクスの行と列を入替えた転置マトリクスです。(3)式の導出は要素剛性マトリクスの導出のページで述べています。

今，Δを次式で定義します。

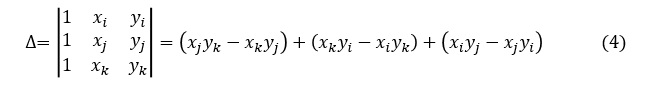
三角形要素の面積は次式で表されます。

変位－ひずみマトリクス［Ｂ］は次式で表されます。

応力－ひずみマトリクス［Ｄ］は次式で表されます。

ここでＥはヤング率，νはポアソン比です。

これで，要素剛性マトリクスが計算できますね。次は全体マトリクスの構築です。

全体マトリクスの構築

説明を簡単にするために，図５に示すような３つの要素で構成される有限要素法モデルを考えます。各節点に番号をつけ，各要素にも番号をつけます。要素番号は丸数字（①②③）で表記します。

有限要素法モデルでは，連続体が分割されて要素となって離散化されているため，境界条件は要素の辺ではなく節点に対して行います。この場合，節点１はｘ方向には動かない境界条件を（ｘ方向の変位拘束），節点２はｘ方向にもｙ方向にも動かない境界条件（ｘ方向の変位拘束とｙ方向の変位拘束）を設定しています。そして，節点５に外力Ｗを設定しています。

節点拘束について注意点があります。有限要素法モデルが剛体変位と回転しなくなるために十分な拘束をする必要があります。今回の場合，節点２についてｘ方向とｙ方向の変位を拘束しているので，有限要素法モデルが剛体変位することはありませんが，これだけでは節点２を中心として回転してしまいます。回転を防止するために節点１のｘ方向変位を拘束しています。拘束が十分でないと後述する逆マトリクスが求まらないことになります。

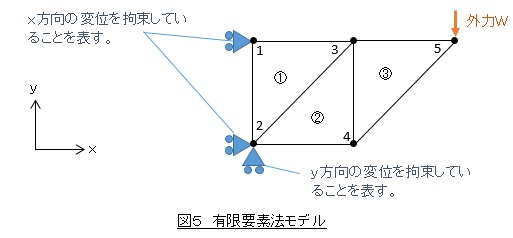
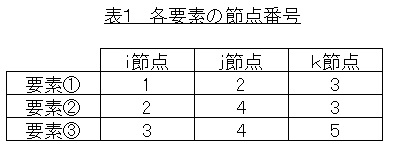
各要素の節点番号を決めます。節点番号は反時計回りにつけますので，要素①のｉ節点は１，ｊ節点は２，ｋ節点は３となります。同様にして各要素の節点番号は表１のようになります。

全体剛性マトリクスを［Ｋ］，全体の変位ベクトルを｛Ｕ｝，全体の外力ベクトルを｛Ｆ｝として，連立方程式を作ります。次式です。

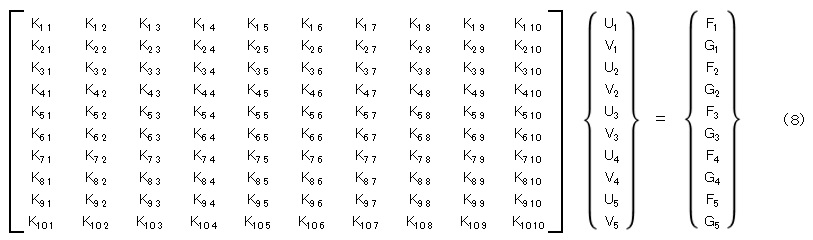
ここで，Ｕ_１は節点１のｘ方向変位，Ｖ_１は節点１のｙ方向変位，Ｆ_１は節点１に作用するのｘ方向の力，Ｇ_１は節点１に作用するのｙ方向の力，．．．．．です。

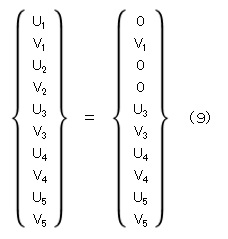
全体の変位ベクトル｛Ｕ｝に値を代入しましょう。

節点１はｘ方向変位が拘束されていますのでＵ_１＝０とします。同様にしてＵ_２＝０，Ｖ_２＝０です。Ｖ_１，Ｕ_３，Ｖ_３，Ｕ_４，Ｖ_４，Ｕ_５，Ｖ_５　は，未知数ですのでそのままにしておきます。全体の変位ベクトル｛Ｕ｝は次式となります。

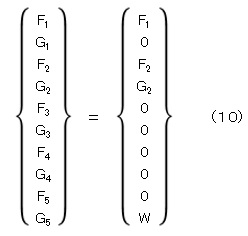
次は全体の外力ベクトルに値を代入ましょう。

節点５のｙ方向外力はＷなのでＧ_５＝Ｗとします。節点１のｙ方向，節点３のｘ方向とｙ方向，節点４のｘ方向とｙ方向，節点５のｘ方向　には外力が作用していませんので，Ｇ_１＝０，Ｆ_３＝０，Ｇ_３＝０，Ｆ_４＝０，Ｇ_４＝０，Ｆ_５＝０　とします。

節点１のｘ方向変位は拘束されています。ということは，拘束支持しているものから何らかの反力（外力）を受けているはずです。しかし，この反力の値は今のところ未知数ですので，節点１のｘ方向外力はＦ_１のままにしておきます。節点２のｘ方向外力，ｙ方向外力についても同様にＦ_２，Ｇ_２のままにしておきます。全体の外力ベクトル｛Ｆ｝は次式となります。

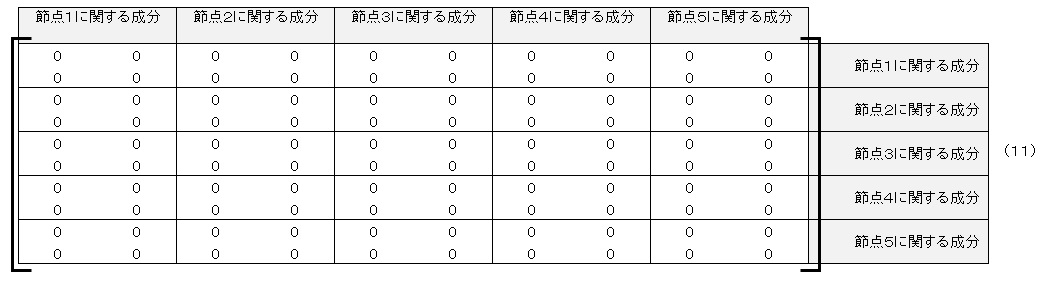
いよいよ，全体の剛性マトリクス［Ｋ］の構築です。

最初に全成分にゼロを代入します。次のようになります。

全体の剛性マトリクスに要素①の剛性マトリクス成分を加えます。表１に示したように要素①は節点１，節点２，節点３からなりますので，節点１，節点２，節点３の座標と材料定数から要素剛性マトリクスを(3)，(4)，(6)，(7)式を使って求めます。求めた要素剛性マトリクスを，全体剛性マトリクスの節点１，２，３に関する成分のところに足し合わせます。要素①の要素剛性マトリクスの成分をｋ①として表現すると，要素①の分を足し合わせた後の全体剛性マトリクスは以下のようになります。

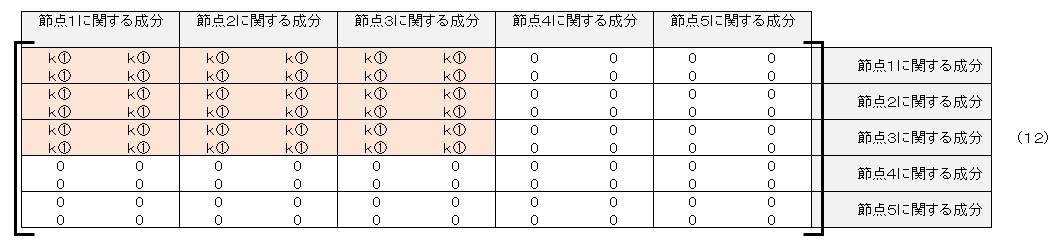
全体の剛性マトリクスに要素②の剛性マトリクス成分を加えます。表１に示したように要素②は節点２，節点４，節点３からなりますので，求めた要素剛性マトリクスを，全体剛性マトリクスの節点２，４，３に関する成分のところに足し合わせます。要素②の分を足し合わせた後の全体剛性マトリクスは以下のようになります。

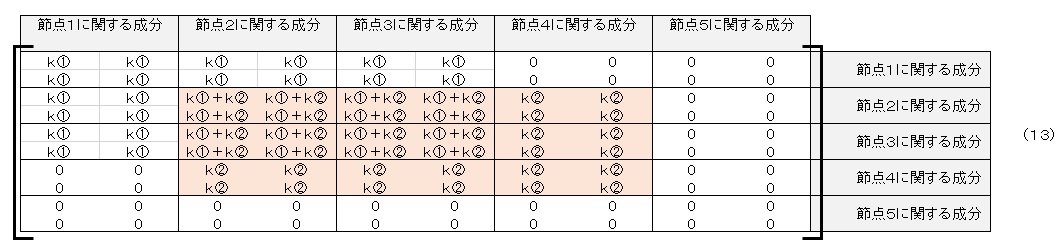
全体の剛性マトリクスに要素③の剛性マトリクス成分を加えます。表１に示したように要素③は節点３，節点４，節点５からなりますので，求めた要素剛性マトリクスを，全体剛性マトリクスの節点３，４，５に関する成分のところに足し合わせます。要素③の分を足し合わせた後の全体剛性マトリクスは以下のようになります。

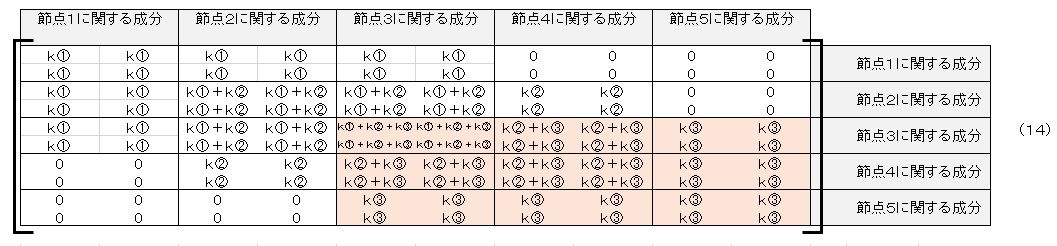
全体剛性マトリクスができあがりました。全体剛性マトリクスには以下の特徴があります。

• 正方マトリクスである。
• 対称マトリクスである。
• ある列について［Ｋ］の成分を合計するとゼロとなり，ある行についても［Ｋ］の成分を合計するとゼロとなる。
• ［Ｋ］の対角成分は正である。
• ［Ｋ］の逆マトリクスは存在しない。

連立方程式の解法

全体の連立方程式をもう一度書きます。説明を容易にするため各成分はｋ①，ｋ②，ｋ③ではなく，Ｋ_１　１，Ｋ_１　２，Ｋ_１　３にして表記します。そして未知数を着色しておきます。

変位が未知数である行を上の方にもっていくために，１行目と１０行目を入れ替えます。全体剛性マトリクスについては，１行と１０行を入れ替えるのは当然としても，１列と１０列も入れ替える必要があります。入れ替えた後の連立方程式を以下に記します。

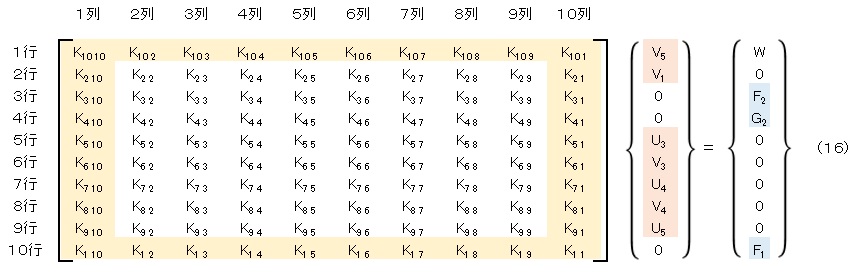
さらに，３行と９行を入れ替えて，４行と８行を入れ替えます。そうすると未知数の変位が上の方に集まり，未知数の外力が下の方に集まります。連立方程式は次式となります。

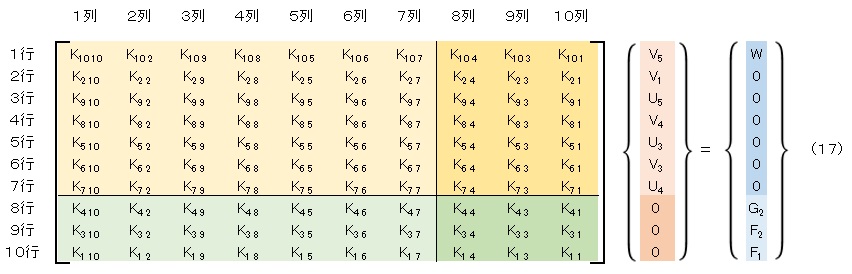
未知数と既知数が分離できました。変位ベクトルを未知数の変位ベクトル｛Ｕ_Ａ｝と既知数の変位ベクトル｛Ｕ_Ｂ｝に分けます。次に外力ベクトルを既知数の外力ベクトル｛Ｆ_Ａ｝と未知数の外力ベクトル｛Ｆ_Ｂ｝に分けます。そして剛性マトリクスを４つのマトリクス［Ｋ_Ａ］，［Ｋ_Ｂ］，［Ｋ_Ｃ］，［Ｋ_Ｄ］に分けます。

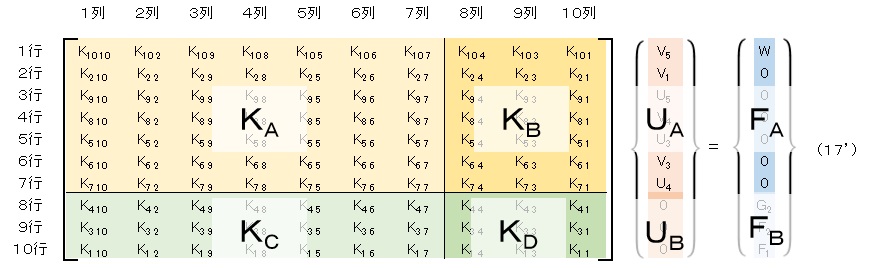
そうすると，(17’)式は次式のようにあらわすことができます。

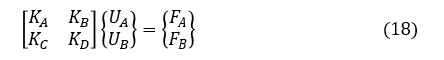
(18)式を次式のように分解します。

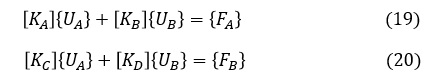
｛Ｕ_Ａ｝が未知数の変位ベクトルですので，これから｛Ｕ_Ａ｝を求めます。(19)式を変形します。

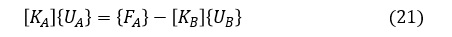
先ほど「［Ｋ］の逆マトリクスは存在しない。」と述べましたが，［Ｋ_Ａ］の逆マトリクスは計算することができます。(21)に対し左から［Ｋ_Ａ］の逆マトリクス［Ｋ_Ａ］^－１を掛けると，未知数である変位ベクトル｛Ｕ_Ａ｝が求まります。

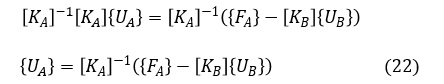
未知数だった各点の変位が求まりました。

｛Ｕ_Ｂ｝の成分はすべてゼロだったのですが，これは図５において変位を拘束したためであります。変位の境界条件に強制変位を設定した場合，｛Ｕ_Ｂ｝の成分は強制変位の値となりますのでゼロでなくなります。

次は拘束点に作用する反力の計算です。｛Ｕ_Ａ｝が既知となりましたので，(20)式の左辺の計算ができるようになりました。これで｛Ｆ_Ｂ｝が求まり，すべての未知数が求まりました。

応力とひずみの計算

応力とひずみは要素ごとに計算します。

要素①について，節点変位｛ｕ｝を抽出します。表１に示したように要素①は節点１，節点２，節点３からなりますので，要素①の変位ベクトル｛ｕ｝は次式になります。

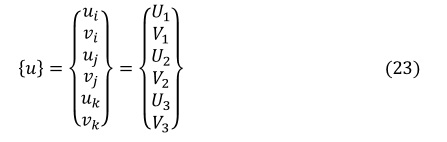
要素の変位ベクトルに，左から(6)式で示した変位－ひずみマトリクス［Ｂ］を掛算すると，ひずみベクトル｛ε｝が求まります。次式となります。この式の導出は，要素剛性マトリクスの導出のページで述べています。

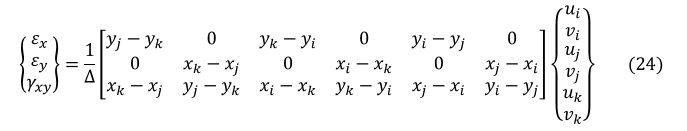
これで各要素のひずみが求まりました。次は応力です。ひずみと応力は次の関係があります。

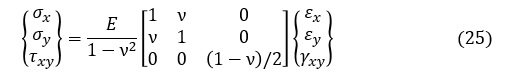
他の要素についても同様に応力とひずみを求めることができます。

以上の過程を踏むことで，弾性体の変位や応力を求めることができます。これが線形解析における有限要素法の手順です。

有限要素法で使われる要素

ここで述べた要素は三角形１次要素です。要素内の変位は(1)式で仮定したように座標の１次式で，応力とひずみは要素内で一定値としたものです。三角形１次要素で真の解に近づけようとすると，かなり細かな要素分割が必要です。要素内の変位を以下に示した２次式で仮定すると，応力とひずみは座標に対して１次式で変化することになり，近似の精度が高まります。このような要素を三角形２次要素と言い，表２にその形状を示します。三角形２次要素では粗い要素分割で真の解に近づけることができます。

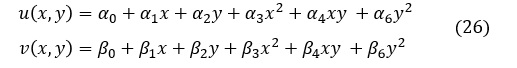
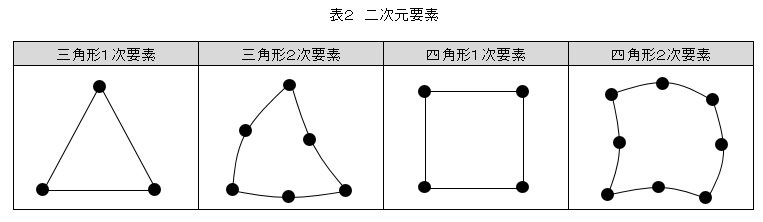
四角形要素にも四角形１次要素と四角形２次要素があり，これらを表２に示します。三角形要素と同様に１次要素では変位は座標の１次式で変化すると仮定されており，２次要素では変位は座標の２次式で変化すると仮定されておりますが，仮定する式が若干異なります。

３次要素にすればより精度の高い変位の近似ができそうですが，計算が煩雑になるなどの理由から普及しませんでした。応力集中部に対しては，二次要素を使って要素分割を細かくする戦略がとられます。

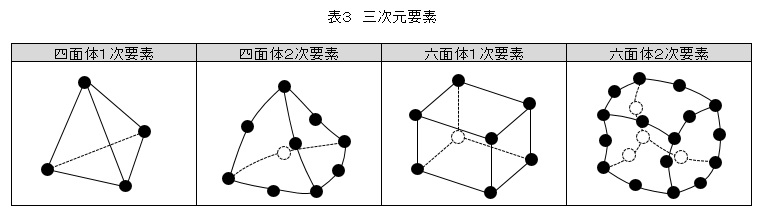
以上は二次元問題の要素ですが，三次元問題の要素についても説明しておきます。三次元問題の要素を表３に示します。１次要素は変位の変化を１次式で近似し２次要素は変位の変化を２次式で近似していますが，四面体要素より六面体要素の方がより高い精度の式で近似しています。要素の自動分割（オートメッシャー）が普及していない時代は六面体要素が重宝していましたが，任意形状の立体をオートメッシャーを使って六面体要素で要素分割することは難しく，オートメッシャーが普及した現在では四面体２次要素が多く使われています。

参考文献

１）戸川，有限要素法概論，培風館，(S56)

２）三好，有限要素法入門，培風館，(S53)

３）Ｏ．Ｃ．ツィエンキーヴィッツ，基礎工学におけるマトリックス有限要素法，吉識，山田　監訳，(S50)