せん断ロッキング　アワーグラスモード

ＨＯＭＥ　＞　ＣＡＥ・有限要素法　＞　せん断ロッキング

ＨＯＭＥ　＞　ＣＡＥ・有限要素法　＞　アワーグラスモード

せん断ロッキング

せん断ロッキングとは，１次要素が曲げの変形を表現できないため，せん断変形成分を過大に評価してしまい，剛性が高い計算結果を出力してしまう現象です。完全積分の１次要素で現れます。

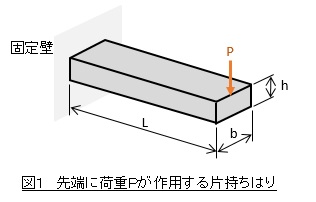
図１に示す片持ちはりの先端変位をモチーフとして，せん断ロッキングを観察してみましょう。片持ちはりの寸法は(1)式，ヤング率Ｅと荷重Ｐは(2)式の値とすれば，先端の変位量は先端に荷重がかかる片持ちはりのページで述べたように，0.8 [mm]となります。使用したソフトはAMSYS Mechanical APDL Ver.17.0で，今は使われていない古い１次要素であるSOLID45を使用しました。要素オプションとして完全積分を選択しました。

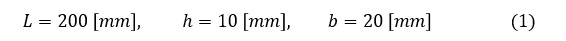
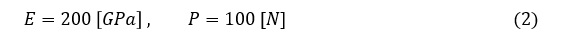
要素分割を図２に示します。６面体１次要素です。

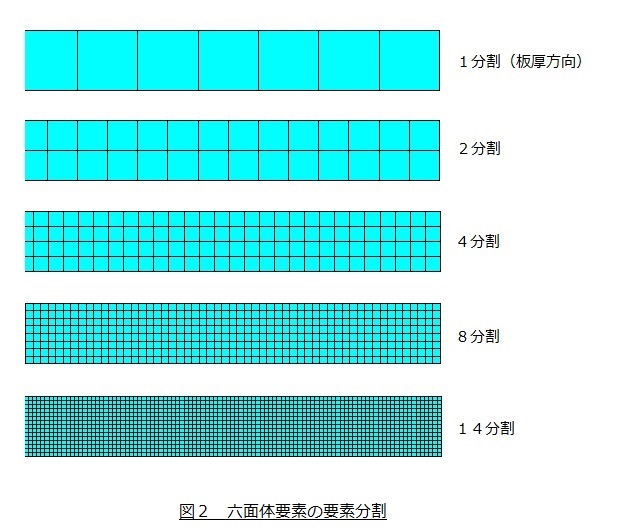
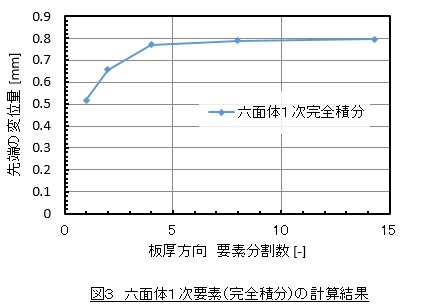
図３に計算結果を示します。要素分割数を増やすに従って先端変位ははり理論の解である0.8[mm]に近づきますが，要素分割数が１分割と２分割の場合の先端変位は小さい値となっており，剛性が高い計算結果となっています。

ANSYSの剛性マトリクスがどのようなアルゴリズムで計算されているかは公開されておらずはっきりしたことは言えませんが，せん断ロッキングの一面を垣間見えたと思います。

低減積分

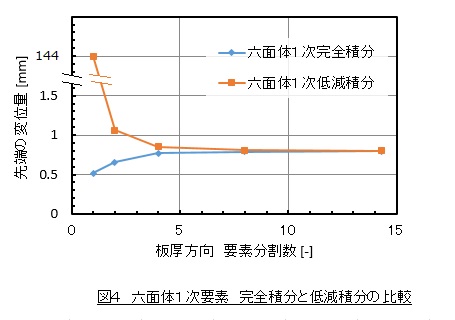
せん断ロッキングの対策として低減積分があります。低減積分とは剛性マトリクスを求めるための数値積分の次数を減じたものです。六面体１次要素の要素オプションを低減積分に変更して計算しました。この結果を図４に示します。

要素分割数が１分割のときは変位が144[mm]ととんでもない値となってしまいましたが，要素分割数を増やすとはり理論の解に近づきました。低減積分の場合は，変位が大きめ，つまり，剛性が低めの計算結果となりました。要素分割数が２分割と４分割の結果を比べると，低減積分にしたからと言って計算精度が上がるとは言えない結果となりました。

２次要素

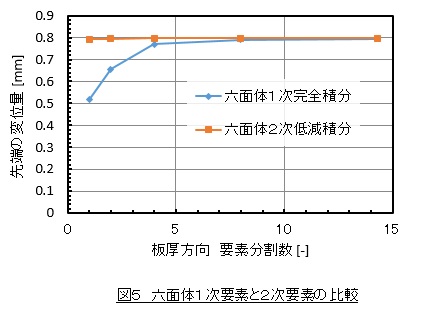
六面体２次要素（低減積分）で計算しました。この結果を図５に示します。要素分割数が１分割で先端の変位量が0.79[mm]とほぼはり理論の解になっています。２次要素は計算コストがかかると言われていますが，１次要素でこれと同じ計算精度を出すためには８分割しなければならず，図２の１分割（中間節点あり）と８分割（中間節点なし）を比較すると，１分割（中間節点あり）の方がはるかに節点数が少なく計算時間がかかりません。

以上のことから，せん断ロッキングの解決策は２次要素の選択ということになります。

実は１次要素にもせん断ロッキングが出ない工夫をしたものがありますが，ソフトによって中身が異なるため比較の対象から外しております。

アワーグラスモード

六面体１次要素で低減積分を選択した場合，アワーグラスモードという物理的には発生しない数学的な安定状態の変形形態が出現します。アワーグラスモードの例を図６に示します。要素の変形形状が砂時計（アワーグラス）のようなものなので，このように呼ばれています。

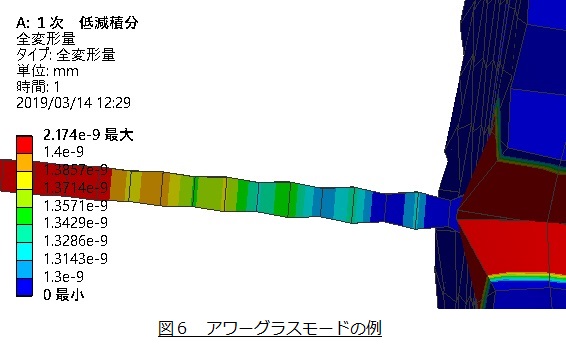
アワーグラスモードは，縦方向と横方向に１要素になるような要素分割をしたときに出現します。対策は，①要素分割を細かくすることと，②２次要素を使用すること，があげられます。

しかし，商用有限要素法ソフトの１次要素はアワーグラスモードが出にくいような工夫がなされていますので，アワーグラスモードで悩まされることはほぼないでしょう。実は，図６のアワーグラスモードを出すのに大変苦労しました。

対策として２次要素を用いて計算した例を図７に示します。問題は解決されています。せん断ロッキングもアワーグラスも２次要素を使用することで解決します。

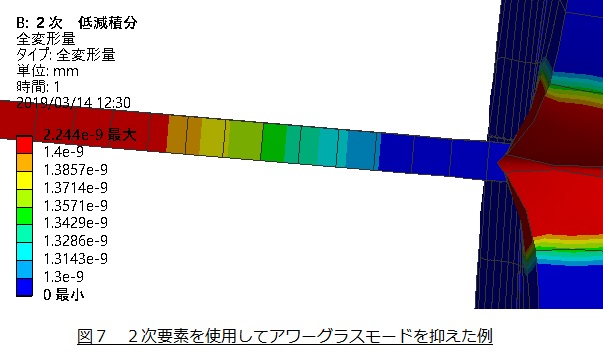
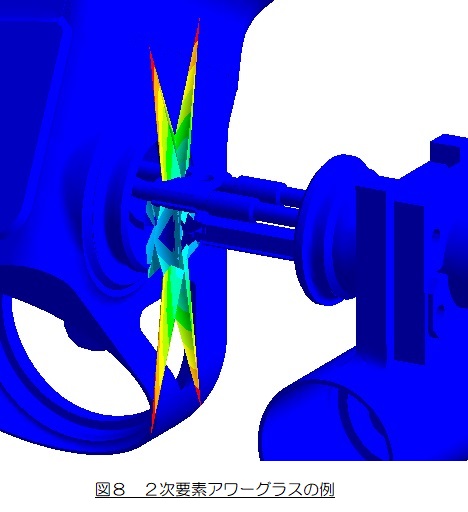
とはいっても私の経験で恐縮ですが，低減積分を選択した２次要素を使ってアワーグラスモードらしき挙動を経験することが年に２，３度あります。このときは要素分割を細かくすることで対処しました。例を下図に示します。