セレンディピティ族要素

ＨＯＭＥ　＞　ＣＡＥ・有限要素法　＞　セレンディピティ族要素

四角形１次の要素剛性マトリクス[k]の導出では，図1に示すようなξ－η座標系の正方形要素を導入します。

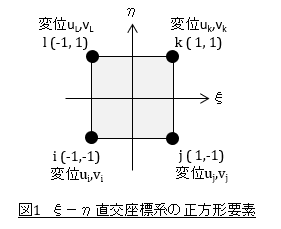
正方形要素内の任意の点（ξ，η）の変位ｕ（ξ，η），ｖ（ξ，η）を次式で定義します。

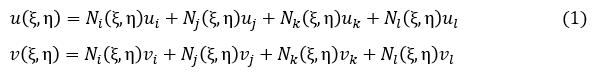
N_i(ξ,η)，N_j(ξ,η)，N_k(ξ,η)，N_l(ξ,η)を形状関数といいます。それでは形状関数の形を決めるわけですが，下記条件が成立すれば都合がいいですね。

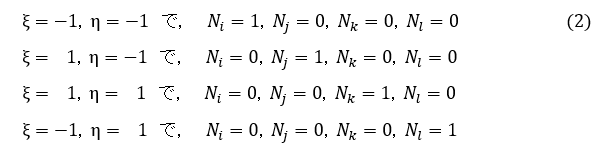
なぜならば

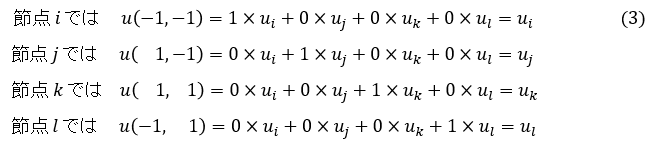
となって，節点位置で変位を再現できるからです。

それでは，N_i(ξ,η)，N_j(ξ,η)，N_k(ξ,η)，N_l(ξ,η)をどのような形にすればよいでしょうか。次式です。

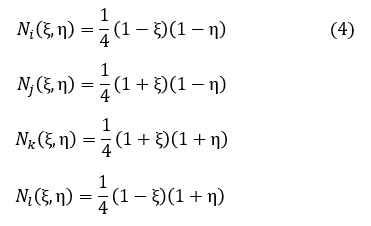
これらの式は，ぱっとひらめいて導出されたことからセレンディピティ族要素と呼ばれています。「セレンディピティ」という言葉とは，「セレンディップの3人の王子」という童話で，セレンデップ（セイロン，今のスリランカですね）の3人の王子が，その洞察力からいろいろなことを発見したことからきています。

四角形２次要素ではどうでしょうか。形状関数は次式となります。

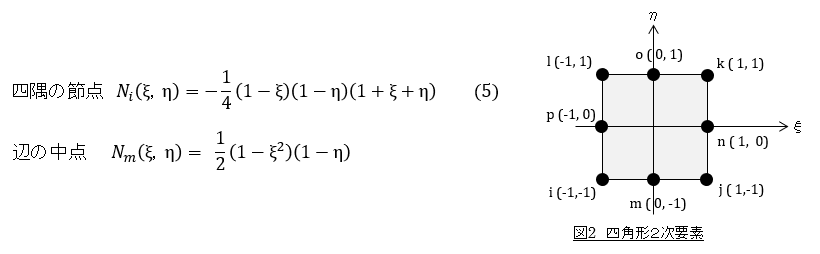
(2)式を洞察力とひらめきで捻出するのはなかなか難しいですね。やっぱり，セイロンの3人の王子の出番が必要なようです。

詳しくは有限要素法の定式化のページを参照してください。