周波数応答解析

ＨＯＭＥ　＞　ＣＡＥ・有限要素法　＞　周波数応答解析

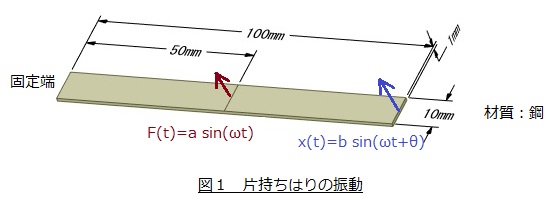
片持ちはりの振動を例にして説明します。図１の示す片持ちはりの中央の線に振幅ａ[N]のsin波状に変化する外力　F(t)=a sin(ωt)　を加えた続けたとします。過渡的な挙動が終わり定常状態になると片持ちはりの先端の変位x(t)もsin波状となります。式で表すと　x(t)=b sin(ωt+θ)　となります。

ここでbは振動変位の振幅，θは位相です。先端の変位x(t)は外力F(t)と同期して変化するわけではなく，時間的にずれて変化します。このずれを表す量が位相θです。θ＝０°のときはx(t)とf(t)は完全に同期しています。つまり，外力f(t)が上方向に作用している瞬間に変位x(t)も上方向に移動しています。θ＝１８０°のときは，外力f(t)が上方向に作用している瞬間に変位x(t)は下方向に移動しています。θ＝９０°のときは，外力f(t)が上方向に作用している瞬間に変位x(t)は停止しています。

外力が加わり続けているときの振動なので，このような振動を強制振動と呼びます。

角振動数ω[rad/s]を２πで割って振動数ｆ[Hz]で議論しましょう。振動数ｆを色々変化させると応答の振幅ｂと位相θが変化します。いろいろなｆ_ｉに対する振幅ｂ_ｉと位相θ_ｉを求める解析が周波数応答解析です。

グラフで表すと図２，図３のようになります。図３は振幅ｂを対数表示にしています。対数表示にすることでピークがとらえやすく，振幅ｂが小さな値のときもその数値を正確にグラフから読取ることができます。一方，振幅ｂを実数表示にするとピーク以外の振幅がほとんどゼロであることが直感的にわかります。実数表示と対数表示の両方を見ることをお勧めします。

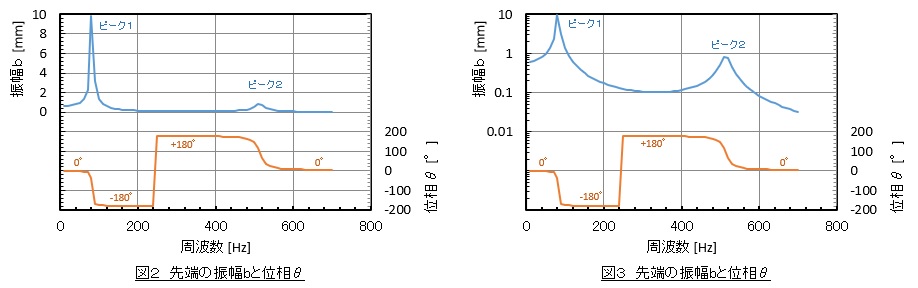
上図で振幅が極大になっているところ（ピークと表記）は共振点で，その周波数は固有振動数ですね。固有振動数はモーダル解析でも求めることができます。ピークの振幅は減衰率で決まるので，周波数応答解析では正確な減衰率を入力しておく必要があります。しかし，減衰率はネットで調べてもあまり載っていないので自分で測定する必要があり，ＦＦＴアナライザ，インパルスハンマ（ないしは加振機），加速度ピックアップなどが必要となります。かなり難しくて面倒な作業です。

今回の例では外力の振幅を１[N]としましたので，図２，図３は周波数応答関数ととらえることができます。系の伝達関数をＨ（ｓ）とすれば，周波数応答関数の大きさは｜Ｈ（ｊω）｜，位相は∠Ｈ（ｊω）です。

応答倍率と共振曲線

周波数ゼロのときの振幅をｂ_staticと表記します。ｂ_staticは周波数応答解析では求まりませんので，荷重をａとした静解析ではりの先端の変位を求める必要があります。ｆ_ｉに対する振幅ｂ_ｉをｂ_staticで割ったものを応答倍率や動的応答倍率と呼んでいます。

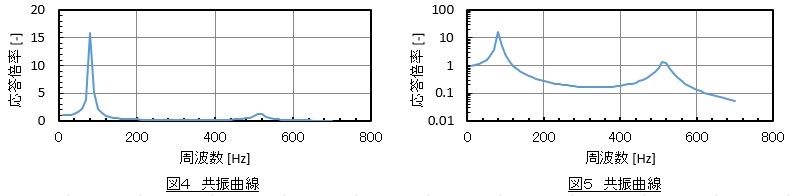
横軸を周波数として応答倍率をグラフで表したものを共振曲線や変位共振曲線と呼んでいます。共振曲線を図４，図５に示します。

モード重ね合せ法とフル法

有限要素法ソフトで周波数応答解析をするときにモード重ね合せ法で計算するかフル法で計算するか選択する必要があります。モード重ね合せ法は事前にモーダル解析を実施して，その結果得られるモーダルパラメータを使って計算します。計算時間が圧倒的に短いのが特徴ですが，現象を十分再現できるだけの振動モードを求めなければならないことに注意が必要です。フル法はモーダル解析を行わず直接計算する方法です。コンピュータの性能が向上した今ではフル法でやった方がいいのかもしれません。

周波数応答解析の入力と出力について

今回のケースでは入力として力を選びましたが，周波数応答解析で入力として設定できるものには力の他に強制変位があります。また，出力として変位を選びましたが出力として得られるものは，変位，速度，加速度，応力，ひずみなどがあります。

出力はモデル全体の分布としてコンタ図として出力できます。60[Hz]で加振したときの変形形状を図６に，500[Hz]で加振したときの変形形状を図７に示します。

60[Hz]で加振したときは加振点（はりの中央）と応答点（はりの先端）は同位相で変形していますが，500[Hz]で加振したときは逆位相であることがわかります。

　　図６　60[Hz]加振　　　　　　図７　500[Hz]加振