要素の種類

ＨＯＭＥ　＞　ＣＡＥ・有限要素法　＞　要素の種類

三次元ＣＡＤで設計しそれを有限要素法ソフトにインポートして解析する方が大半だと思いますので，三次元要素を中心に説明していきます。

三次元ソリッド要素

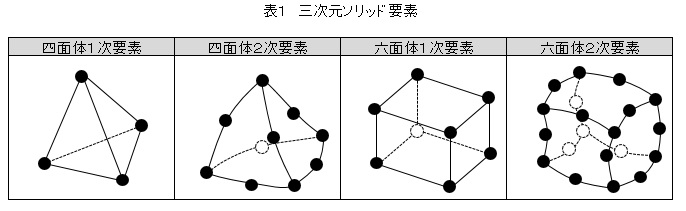
ＣＡＤデータをインポートして要素分割した場合，三次元ソリッド要素を使った有限要素法モデルが生成されます。三次元ソリッド要素を表１に示します。要素分割のときの注意点があります。必ず２次要素（中間節点あり）で分割してください。１次要素と２次要素のページで詳しく述べますが，１次要素と２次要素とでは計算精度が格段に違います。

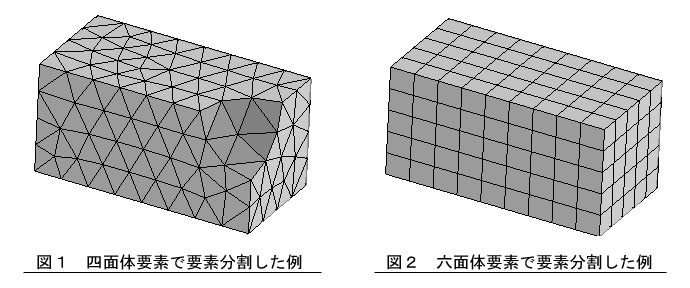
四面体要素で要素分割した例を図１に，六面体要素で要素分割した例を図２に示します。

四面体要素を用いた場合，任意の形状の三次元モデルを要素分割できますが，六面体要素の場合，三次元モデルの形状に制約が生じ，六面体や多角形を掃引した形状に対してだけ要素分割ができます。図２のような形状は六面体要素で分割できますが，図１のような形状は六面体要素で分割できません。

変位の自由度は，Ｘ方向並進，Ｙ方向並進，Ｚ方向並進の３自由度となります。

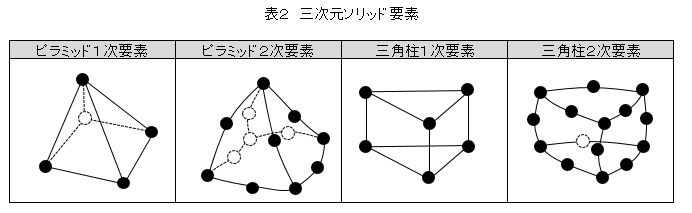
三次元ソリッド要素には，表２に示したような要素もあります。ピラミッド要素は六面体要素と四面体要素を結合するために使われます。三角柱要素は多角形平面を掃引して生成した三次元モデルをスイープメッシュしたときに生成されます。

三次元シェル要素

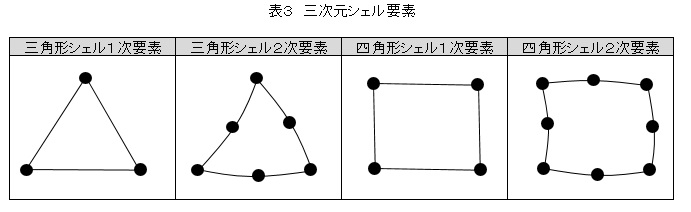
薄い板による構造物を解析するときには三次元シェル要素を使います。三次元シェル要素を表３に示します。三次元形状モデルはソリッドモデルではなく面の集合体としたモデルを準備する必要があります。最近は，ソリッドモデルから中立面を抽出する機能を持つソフトも出ています。シェル要素の場合，材料定数の他に板厚に関する情報を有限要素法ソフトに入力する必要があります。ソリッド要素と同様に二次要素を使ってください。

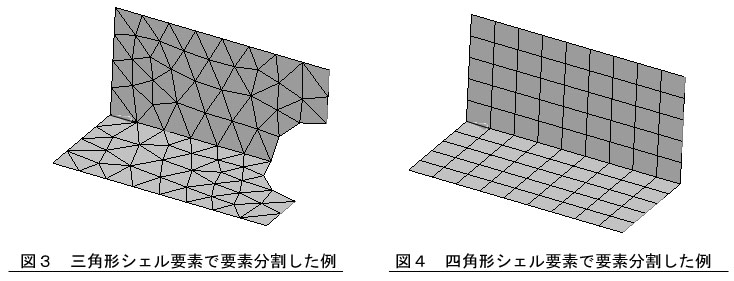
三角形シェル要素で要素分割した例を図３に，四角形シェル要素で要素分割した例を図４に示します。

最近のメッシャーでは，ほぼ形状の制約なく四角形シェル要素で要素分割ができます。

変位の自由度は，Ｘ方向並進，Ｙ方向並進，Ｚ方向並進に加え，Ｘ方向回転，Ｙ方向回転の５自由度となります。

三次元ビーム要素

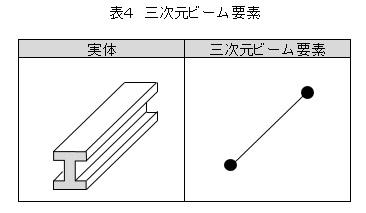
骨組み構造物を解析するときには三次元ビーム要素を使います。三次元ビーム要素を表４に示します。三次元形状モデルはソリッドモデルではなく線の集合体としたモデルを準備する必要がありますが，有限要素法ソフトのプリプロセッサでモデリングすることが多いです。ビーム要素の場合，材料定数の他に断面二次モーメントと断面係数に関する情報を有限要素法ソフトに入力する必要があります。任意形状の断面二次モーメントを計算するソフトを作りました。よかったら使ってみてください。

変位の自由度は，Ｘ方向並進，Ｙ方向並進，Ｚ方向並進に加え，Ｘ方向回転，Ｙ方向回転，Ｚ方向回転の６自由度となります。

ビーム要素の場合，はりの曲げ理論で求まる応力と変位が出力されますので，その応力は応力集中成分を含まない公称応力となります。

三次元ソリッド要素，三次元シェル要素，三次元ビーム要素の混在

三次元ソリッド要素，三次元シェル要素，三次元ビーム要素を混在させて解析することは可能です。着眼点はソリッド要素を用い，着眼点でないところはシェル要素やビーム要素を用いると，要素数と節点数を劇的に減らすことができ，計算時間の短縮につながります。しかし，三次元ソリッド要素と三次元シェル要素の結合には，シェル要素の板厚の半分をオフセットさせるところや，節点共有で結合しますが結合している節点へどのようにモーメント荷重を伝達させるかなどに工夫が必要です。ビーム要素との結合でも同様の工夫が必要となります。

二次元要素

問題を二次元問題としてとらえて，二次元要素を用いることができます。二次元要素には，平面応力状態を解く要素，平面ひずみ状態を解く要素，軸対称二次元要素などがあります。軸対称二次元要素とは，回転体の形状をした三次元モデルに円周上に均一に荷重と変位拘束が設定できる場合に使用します。共に２次要素の使用を勧めます。これらの要素を使うと計算時間を劇的に短くすることができますが，コンピュータの性能が向上している今となっては，無理して二次元問題にする必要はないと考えております。

変位の自由度は，Ｘ方向並進，Ｙ方向並進の２自由度となります。