公称応力ベースの疲労評価

ＨＯＭＥ　＞　強度計算　＞　公称応力ベースの疲労評価

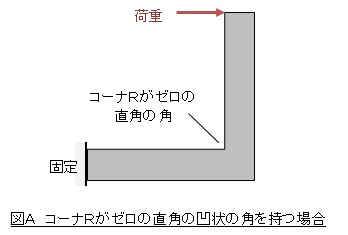
応力集中が激しい場合（軟鋼でα＞２．５，合金鋼でα＞３．５の場合や，図ＡのようにコーナＲがゼロの直角の凹状の角を持つ場合）や，き裂状の切欠がある場合の疲労強度の評価法を説明します。評価法を説明した後，計算例を述べます。

強度評価の最も確実な方法は，製品を使い製品と同じ環境で，引張強さ，疲労強度を求めることです。次に確実な方法は，製品からテストピースを削りだしてテストピースを作り，製品と同じ環境で，引張強さ，疲労強度を求めることです。この場合，切欠係数βを用意する必要があります。ついでに，下限界応力拡大係数範囲⊿Ｋｔｈを実験的に測定しておけば，問題は解決です。

以上のような厳密なことを主張していては設計が進まないですね。では少々長くなりますが説明を始めます。

基本的な考え方は，応力集中を考慮しないで求めた公称応力ないしはホットスポット応力と許容応力を比較することで疲労破壊の有無を予測します。

手順

疲労強度の評価は下記手順で進めます。

　１．許容応力σ_alを求める。

　２．応力振幅σａと平均応力σｍを求める。

　３．疲労限度線図を作成して，疲労破壊の有無を予測する。

手順１　許容応力σ_alの求め方

許容応力σ_alは次式で求めます¹⁾。

ここで，

　σｗ：両振り荷重（応力比Ｒ＝－１）での疲労強度[Pa]

　ζ１：寸法効果による疲労強度の低下率[-]　０．８～１．０

　ζ２：表面状態，加工履歴，腐食環境，熱処理，使用温度などによる疲労強度の低下率[-]

　β：切欠き係数[-]

　ｆｍ：材料強度の不確実性を補うための安全率[-]

　ｆｓ：荷重見積りの不確実性と応力計算の近似性などに対する安全率[-]

手順１－１　疲労強度σｗについて

鉄鋼材料は疲労限度が現れますので，無限回の繰返し荷重に耐える応力振幅を疲労限度と呼びます。疲労限度が現れる理由は，繰返し荷重によってできた0.1[mm]程度のき裂の進展が止まる（き裂の停留）からとのことです。疲労限度が現れない材料については，１０^６回程度の繰返し荷重に耐える応力振幅を，このサイトに限って「疲労強度」と呼ぶことにします。

疲労強度は材料メーカから入手したり材料試験をして求めますが，入手できなかった場合は引張強さから推定できます。疲労強度と引張強さはほぼ比例関係にあることを利用します。疲労強度の求め方を参照してください。また，金属材料は文献¹⁾に豊富なデータがあります

材料メーカに問合せる際，試験条件も聞いておく必要があります。ポイントは，「両振り荷重か，片振り荷重か」，「引張圧縮試験か，回転曲げ試験か」，「明確な疲労限度が現れたか」などです。回転曲げ試験による疲労強度が得られた場合，引張圧縮試験によるデータに変換しなければなりません。その方法も疲労強度の求め方で述べています。

疲労試験片について述べます。試験片は，鏡面ないしそれに近い研摩仕上げ，ないしは電解研摩をし，加工ひずみ除去のための焼鈍し（６００℃，１時間，真空）が施されています。また試験片の多くは直径１０[mm]の円柱です。実際の部品と状況が異なりますね。この点に注意が必要です。

手順１－２　寸法効果による疲労強度の低下率ζ１について

部品の寸法が大きくなるとその疲労限度が低くなる現象を寸法効果と呼びます。この第一の要因としては，素材の熱処理における質量効果などのように素材の製造過程の違いによって生じる強度の低下があります。第二の要因としては，疲労によるき裂は，微小な欠陥部か金属間化合物などの第二相粒子から発生するとの報告があり，材料の体積が大きいほど欠陥や第二相粒子が存在する確率が高まり，き裂ができやすくなって強度が低下します。「疲労破壊の最弱リンク説」と呼ばれています。

上述したように疲労試験片は直径10[mm]ですので，直径が10[mm]のときはζ１＝１とします。部品の板厚や直径が10[mm]を超えるときはζ１＜１とする必要があります。一方，板厚や直径が10[mm]未満のときはζ１＝１とします。

回転曲げ試験のデータしか手元にありませんでしたが，ζ１の実験データの大多数は図１の着色した領域に位置します。つまり，ζ１は０．８～１．０の値をとります。ζ１として線Ｄと線Ｅの値をとるとしましょう。例えば板厚や直径が３０[mm]のときのζ１は０．８８となります。

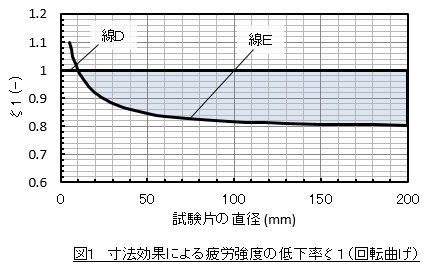
手順１－３　表面状態，加工履歴，腐食環境，熱処理，使用温度などによる疲労強度の低下率ζ２について

上述したように疲労試験片の表面は鏡面，ないしそれに近い研摩仕上げ，電解研摩などが施されています。これに対し実際の部品は切削加工仕上げなどで表面あらさが異なります。また，疲労試験片は焼鈍し処理が施されますが，実際の部品に同様の処理が施されることは稀です。このように，表面状態（加工），腐食環境，熱処理，使用温度などの影響を考慮する必要があります。ζ２の対象としては以下の要因があります。

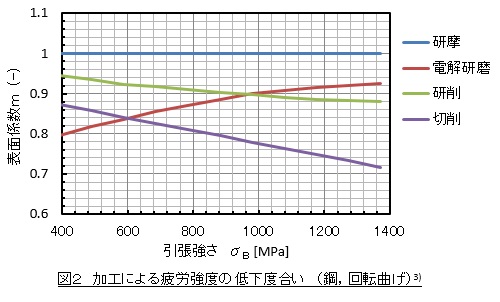
表面仕上げ：切削，研削，電解研摩で，ζ２は１以下の値となります。文献³⁾によると，(2)式で定義される表面係数ｍは図２のようになります。表面係数は，任意の表面粗さでの疲労強度σｗ^Ｒと表面あらさが１μｍ以下，ないしは研摩仕上げ試験片の疲労強度σｗ^{Ｒ＜１μｍ}の比です。ζ２の要因が表面仕上げだけなら，ζ２＝ｍとなります。しかしここで提案があります。加工によってできる表面粗さを小さな切欠きとしてとらえ，この影響をβに含めるといった発想です。つまり，「部品の表面には，切削，研削加工により生じた小さな切欠きと，設計意図に従って作った切欠がある。」という発想です。今回の場合，βを２．４ないし３．４と大きな値を採用している（後述します）のでこの発想が適用できて，表面係数ｍを考慮する必要がなくなります。

表面欠陥：き裂，砂きず，偏析割れ，打こん，圧こん，工作きず，焼割れ，研摩割れ，溶接欠陥などによる影響で，ζ２は１以下の値となります。表面欠陥についても，これらを小さな切欠きとしてとらえ，この影響をβに含めるといった発想があります。今回の場合，βを２．４ないし３．４と大きな値を採用しているのでこの発想が適用できて，表面欠陥の影響をを考慮する必要がなくなります。

腐食性の液体や気体との接触：応力腐食割れ（SCC, stress corrosion cracking）など，腐食環境では疲労強度は大幅に低下します。多くの論文やデータがありますが，実際に自身で実験して確認することをすすめます。耐食性のある材料を選ぶ（特殊なステンレス鋼ですね）か，腐食環境を変えるという選択肢もあると思います。

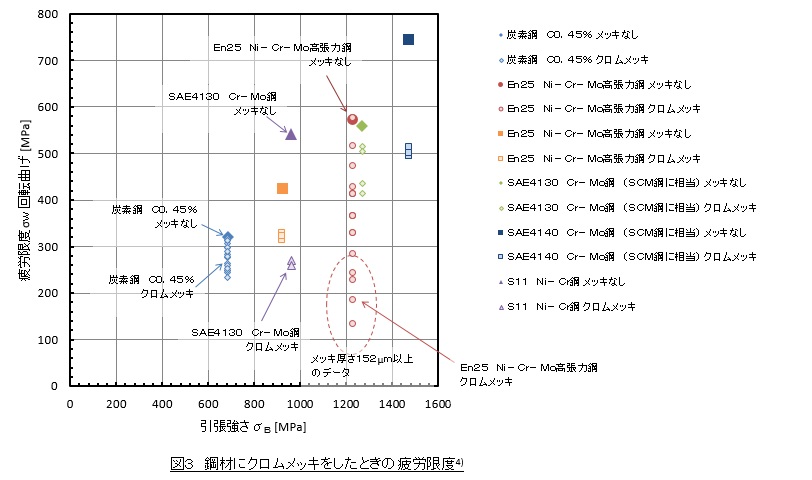
被覆：メッキ，塗装，アルマイト処理などにより疲労強度は低下します。鉄鋼材料の場合，さび防止のためにクロムメッキやニッケルメッキを使用しますが，ともに疲労強度を低下させます。理由は，メッキによる引張の残留応力と，メッキ表面に多数のき裂が存在するためです。鋼材にクロムメッキをしたときの疲労限度を図３に示します⁴⁾。引張強さが低い鋼の場合はメッキによる疲労限度低下の度合いは少ないのですが，引張強さが高い鋼は疲労限度低下の度合いが大きいです。注意が必要です。

表面冷間加工：ショットピーニング，表面圧延などの加工のことてす。表面に圧縮の残留応力を発生させるので，疲労強度は向上します。

表面硬化処理：高周波焼入れ，窒化，浸炭などで，疲労強度は向上します。

その他：フレッチングは注意すべき問題です。疲労強度が１／２～１／３になります。

手順１－４　切欠係数βについて

問題は，切欠先端の曲率半径がゼロであるき裂の切欠係数βの値はいくらかということです。文献⁵⁾にその答えがありました。軟鋼の場合β＝２．４で，引張強さが大きな合金鋼の場合β＝３．４とのことです。この値を採用することにします。切欠先端の曲率半径がゼロでないけれども応力集中が激しい場合も，同様のβの値を採用しておけば問題ないと思います。

手順１－５　材料強度の不確実性を補うための安全率（ｆｍ）

安全率については別のページで説明しております。

疲労強度，寸法効果については低めの値を採用すること，表面状態（加工と表面欠陥）に対してはき裂のβを採用することで，ｆｍを１に近づけられます。しかし，腐食環境，被覆（メッキ，塗装，アルマイトなど），熱処理，使用温度，フレッチングなどの要因が入ると不確定性が増大し大きなｆｍをとらざるを得ません。

手順１－６　荷重見積りの不確実性と応力計算の近似性などに対する安全率（ｆｓ）

荷重の見積りが間違っていたらどうしようもありませんね。しっかりやりましょう。有限要素法で機械の稼働状態の応力を計算するときの注意点を記します。機械が動いているときの荷重だけを境界条件とするのは，危険側の見積りとなります。実は機械が止まっているときも，応力が発生しています。例えば自重やボルトによる締結力です。特にボルト締結部はボルト側に降伏応力の７０[%]程度の締付け力が発生していますので，部品側もそれに応じた圧縮応力が作用しています。ボルト締結部の有限要素法によるモデル化の方法を参考にしてください。

応力計算の近似性に関しては，有限要素法を用いてＶ＆Ｖを実行することで大幅に解決できそうです。

手順１－７　ｆｍ・ｆｓの値

問題は，ｆｍ・ｆｓとしてどんな値を採用するかです。文献¹⁾によると，自動車や鉄道車両など，かなり確実な材料強さの試験値および正確な使用応力の測定値ならびに計算値を基に設計がなされ，かつ多くの実績がある場合は，ｆｍ・ｆｓ＝１．２～１．３程度の値が採用されているとのことです。しかし，多くの場合確実な数値を持ち合わせていることは少ないと思いますので，ｆｍ・ｆｓはより大きな値をとらざるを得ません。私の経験が参考になるかわかりませんが，腐食環境，被覆（メッキ，塗装，アルマイトなど），熱処理，使用温度，フレッチングなど要因がない場合，ｆｍ・ｆｓ＝２としていました。

以上が，許容応力σ_alの求め方です。

手順２　応力振幅σａと平均応力σｍの求め方

①２種類の応力解析を行います。ひとつ目は最大応力σｍａｘが発生するような荷重条件による解析で，ふたつ目は最小応力σｍｉｎが発生するような荷重条件による解析です。

②応力を評価する点（評価点）を決めます。後述する応力振幅σａが最大となる点や平均応力σｍが最大となる点などです。この他には設計者が注目している点も評価点になります。

③最大応力σｍａｘを求めます。最大応力は，最大応力が発生するような荷重条件による解析結果から②で決めた評価点の第一主応力（最大主応力）のホットスポット応力を読取ります。なぜホットスポット応力かというと，今回はき裂状の切欠がある場合を想定していますので，このような点は応力特異点となって，有限要素法によって正確な応力が求められないからです。ホットスポット応力は公称応力とほぼ等しいので，公称応力の代用とします。

④最小応力σｍｉｎを求めます。最小応力は，最小応力が発生するような荷重条件による解析結果から評価点の第三主応力（最小主応力）のホットスポット応力を読取ります。

⑤応力振幅σａと平均応力σｍは次式で求めます。

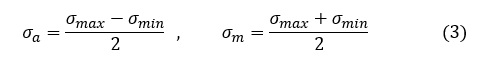
手順３　疲労限度線図を使った疲労破壊の有無の予測方法

疲労限度線図として修正グッドマン線図を使います。下記手順で進めます。

①下記数値を準備します。

　許容応力σ_al，引張強さσ_Ｂ，降伏応力σｙ，安全率　ｆ＝ｆｍ・ｆｓ，
　評価点の応力振幅σａ，評価点の平均応力σｍ

②グラフ用紙を用意し，Ｘ軸とＹ軸を書きます。Ｘ軸を平均応力σｍ，Ｙ軸を応力振幅σａとします。今はグラフ用紙ではなくてエクセルの散布図ですね。

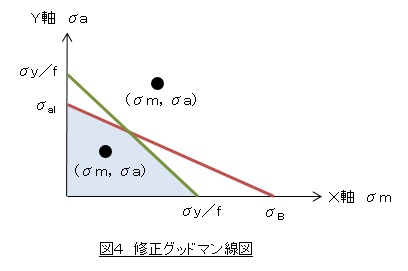
③Ｘ軸切片をσ_Ｂ，Ｙ軸切片をσ_alとした１次直線を書きます。言い換えると，座標（σ_Ｂ，０）と（０，σ_al）を通る直線を引きます。図４の赤線です。

④Ｘ軸切片をσｙ／ｆ，Ｙ軸切片をσｙ／ｆとした１次直線を書きます。言い換えると，座標（σｙ／ｆ，０）と（０，σｙ／ｆ）を通る直線を引きます。図４の緑線です

⑤座標（σｍ，σａ）の位置にプロットします。図４では黒丸（●）です。

⑥図４の水色で表示した領域が疲労破断かつ降伏しない領域で，この領域に⑤でのプロットが入れば大丈夫です。この領域の外にプロットがあるときは設計変更が必要です。

計算例

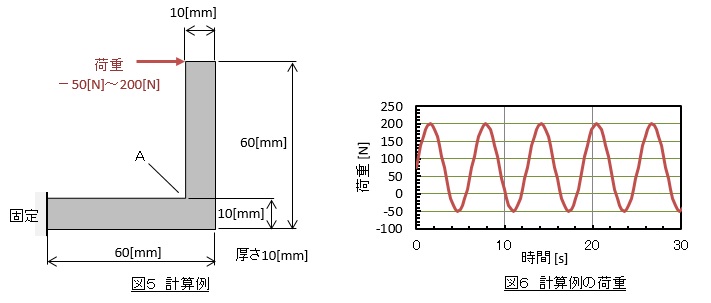
図５のようなＬ金具に，－５０[N]から２００[N]まで変動するの荷重（図６）が作用しているときの，Ａ点の疲労破壊の有無を予測しましょう。Ａ点はコーナＲがゼロの応力特異点で有限要素法では応力が定まらず，激しい応力集中が発生すると予測されます。設計条件は以下とします。

　Ｌ金具の材質はＳＵＳ３０４，切削加工で製作，腐食環境のない室温で使用，表面処理なし

許容応力σ_alの計算

両振り荷重での疲労強度σｗを求めます。
ＳＵＳ３０４材の引張強さσ_Ｂは520[MPa]，降伏応力σｙは205[MPa]です。疲労強度の求め方のページで説明したようにオーステナイト系ステンレス鋼のσｗは次式で求まります。ここでＣは，回転曲げ試験による疲労強度を引張圧縮試験による疲労強度に変換する定数です。

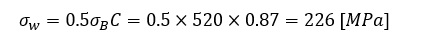
ζ１を決めます。
板厚が10[mm]なので図１から，ζ１は１となります。

ζ２を決めます。
後述するように切欠係数βを２．４としますので，切削加工による表面粗さや表面欠陥を小さな切欠きとしてとらえ，これによる疲労強度低下分はβに含めることができると考えます。また，室温で使用され腐食環境ではなく素材のまま使用するため，ζ２は１とします。

切欠係数βを決めます。
引張強さは低く軟鋼と同レベルと判断してβ＝２．４を採用します。

安全率ｆ＝ｆｍ・ｆｓを決めます。
根拠はありませんが，私の経験からｆ＝ｆｍ・ｆｓ＝２とします。

(1)式に上記数値を代入して許容応力σ_alを以下のように求めます。

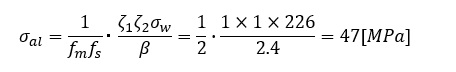
応力振幅σａと平均応力σｍの計算

評価点を決めます。壊れるとすれば明らかにＡ点からき裂が発生すると予測されるため，評価点をＡ点とします。

最大応力σｍａｘを求めます。荷重が200[N]のときのＡ点の第一主応力でのホットスポット応力が最大応力ですので，この条件で応力解析を行います。

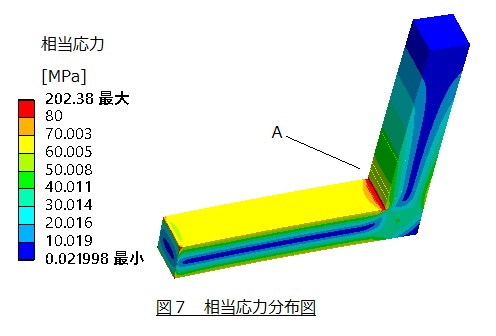
図７は，相当応力分布図です。Ａ点に激しい応力集中が発生しています。Ａ点は応力特異点なのでＡ点の応力を読取っても意味がありません。

解析結果から。図８のＢ線上の第一主応力を抽出しグラフ化します。これを図９に示します。このグラフからホットスポット応力を求めます。ＳＲ２０２　Ｂ法では，Ａ点から板厚の０．５倍離れた点の応力と１．５倍離れた点の応力から外挿してＡ点の応力を求めます。図９の緑色のプロットで示します。この方法によるホットスポット応力は57[MPa]となりました。０．３ｔ法では，Ａ点から板厚の０．３倍離れた点の応力をホットスポット応力とします。図９の赤色のプロットで示します。この方法によるホットスポット応力は53[MPa]となりました。今回はＳＲ２０２　Ｂ法による結果を採用することにします。

以上の検討から，第一主応力であらわした最大応力σｍａｘは57[MPa]となりました。

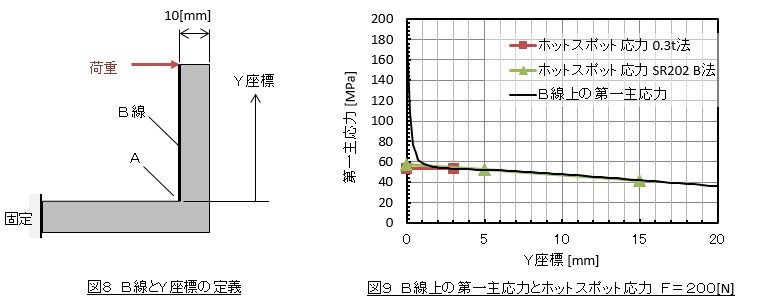
最小応力σｍｉｎを求めます。荷重が-50[N]のときのＡ点の第三主応力でのホットスポット応力が最小応力ですので，この条件で応力解析を行います。第一主応力ではなく第三主応力であることに注意してください。

上述した方法で最小応力を求めた結果，-14[MPa]となりました。

(3)式に従って，応力振幅σａと平均応力σｍを求めます。以下のようになりました。

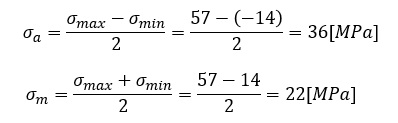
修正グッドマン線図の作成

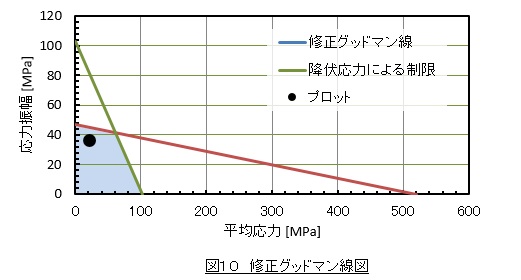
引張強さσ_Ｂは520[MPa]，許容応力σ_alは47[MPa]でしたので，図１０に示すＸＹ座標系において，座標（520，0）と（0，47）を結ぶ線を引きます。これが疲労限度線図になります。

降伏応力σｙは205[MPa]，安全率はｆ＝ｆｍ・ｆｓ＝２なので，σｙ／ｆ＝103[MPa]となりますので，ＸＹ座標系において座標（103，0）と（0，103）を結ぶ線を引きます。これが降伏応力による制限線となります。

最後に，応力振幅σａが36[MPa]，平均応力σｍが22[MPa]でしたので，ＸＹ座標系において座標（22，36）の点をプロットします。

図１０を見るとプロットは着色した領域内に入っていますので，疲労破壊しなくてかつ降伏もしないと考えられます。

以上が，き裂があったり激しい応力集中が発生する部材の公称応力ベースの強度評価法です。

参考文献

１）日本機械学会，疲労強度の設計資料　Ⅰ　一般，寸法効果，切欠効果，(S63)

２）日本機械学会，機械工学便覧　Ａ４　材料力学，(1984)

３）北川，材料の表面と疲れ　（１），生産研究，第17巻　第5号，(1965)

４）日本機械学会，疲労強度の設計資料　Ⅱ　表面状態，表面処理，(1990)

５）大内田，人工き裂のある軸材の疲れ強さ（続報），機械学会論文集，第23巻　第135号，p842，(S32)