修正グッドマン線図

ＨＯＭＥ　＞　強度計算　＞　修正グッドマン線図

図１はある部品に作用する応力の時間変化です。σ_ｍａｘとσ_ｍｉｎは手計算か有限要素法で求めるとして，平均応力σ_ｍと応力振幅σ_ａは次式で定義されます。

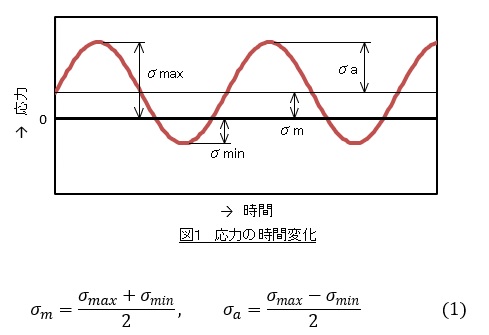
話がそれますが，有限要素法でσ_ｍａｘとσ_ｍｉｎを求めるときは相当応力ではなく主応力を使うべきです。最小応力σ_ｍｉｎが圧縮応力の場合マイナス値となるので，圧縮応力でもプラス値として出力する相当応力では都合が悪いからです。σ_ｍａｘは第一主応力（最大主応力）から読取り，σ_ｍｉｎは第三主応力（最小主応力）から読取ってください。

平均応力がプラス値（引張応力）のときの疲労強度（鉄鋼材料の場合，疲労限度）が平均応力がゼロのときの疲労強度よりも小さくなることは，容易に想像できますね¹⁾。この関係を図で表したもののひとつに修正グッドマン線図（修正Ｇｏｏｄｍａｎ線図）があります。

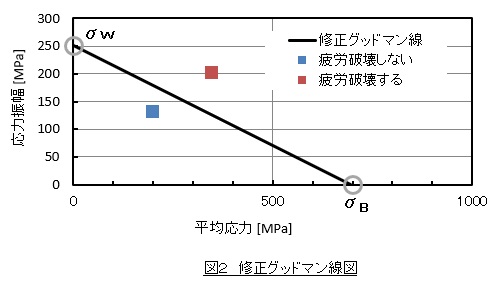
図２に修正グッドマン線図を示します。Ｘ軸切片を引張強さσ_Ｂ，Ｙ軸切片を疲労強度σ_ｗとして直線を引いたものが修正グッドマン線となります。(1)式で平均応力と応力振幅を求め，それを修正グッドマン線図にプロットします。プロットの位置が修正グッドマン線より下にあれば疲労破壊しないと判断でき，上にあれば疲労破壊すると判断します。

安全率を考慮した修正グッドマン線図

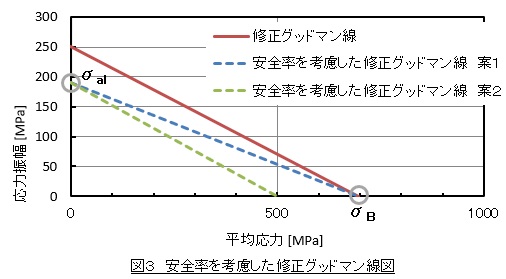
設計では安全率を考慮した修正グッドマン線図を用いることになります。これを図３に示します。安全率を考慮した修正グッドマン線図には２つの案があります。Ｙ軸切片は安全率や切欠係数を考慮した許容応力σ_ａｌですが，Ｘ軸切片については引張強さσ_Ｂとする案（案１）とＸ軸切片側にも安全率を考慮する案（案２）があります。

私は案１を使って仕事をしております。理由は切欠係数を変化させて疲労限度を調べた実験において案１に近い挙動を示すデータが報告されているからです²⁾。

塑性変形の考慮

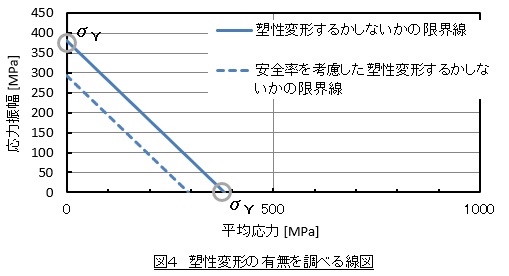
部品が塑性変形しないように設計することも重要です。図４に塑性変形の有無を調べる線図を示します。塑性変形するかしないかの限界線は，横軸の切片を降伏応力σ_ｙ，縦軸の切片も降伏応力とした直線です。平均応力と応力振幅のプロットが塑性変形するかしないかの限界線より下にあれば塑性変形せず，上にあれば塑性変形します。この線についても安全率を考慮します。

設計で使う線図

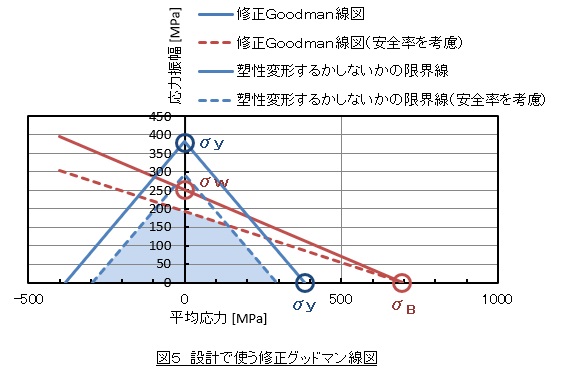
機械の設計では部品が疲労破壊しないことと塑性変形しないことの両方を考慮する必要があるので，図３と図４を重ねた線図を使っています。これを図５に示します。塑性変形するかしないかの限界線を図の青色の実線に示します。安全率を考慮しなれけばなりませんので，切片を降伏応力／安全率とした線（青色の破線）を引きます。次に修正グッドマン線（赤色の実線）と安全率を考慮した修正グッドマン線（赤色の破線）を引きます。設計で使用可能な応力範囲は，青色の破線と赤色の破線に囲まれた水色で着色した領域になります。

疲労限度線図のページも参考にしてください。修正グッドマン線図を使った計算例は，繰返し荷重が作用する場合と公称応力ベースの疲労評価のところで紹介しています。

参考文献

１）西原，櫻井，繰返引張圧縮應力を受ける鋼の強さ，日本機械学會論文集，(S14)

２）北川英夫，材料の表面と疲れ(2)，生産研究，18 巻　1号，(1966)