低サイクル疲労，マンソンーコフィン則

ＨＯＭＥ　＞　強度計算　＞　低サイクル疲労

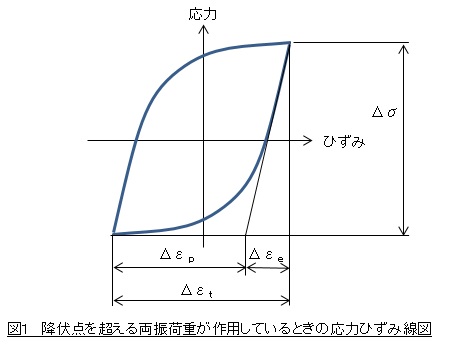
荷重の繰返し数が１０^４回以下で破壊する疲労現象を低サイクル疲労(low cycle fatigue)といいます。このような疲労では応力やひずみは降伏点を超えている場合がほとんどです。降伏点を超える両振荷重が作用しているときの応力ひずみ線図を図１に示します。図において，Δε_ｔは全ひずみ範囲，Δε_ｐは塑性ひずみ範囲，Δε_ｅは弾性ひずみ範囲，Δσは応力範囲です。範囲という言葉を使いましたが，これは振幅ではなく（最大値－最小値）を指します。

Δε_ｔ，Δε_ｐ，Δε_ｅ，Δσの間には次式の関係があります。Ｅはヤング率です。

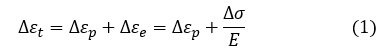
荷重の繰返し数が１０^４回以下において，Δε_ｐと破断繰返し数Ｎ_ｆの関係を対数グラフ上にプロットすると直線となって，その関係を次式で表すことができます。

(2)式の関係をマンソンーコフィン則(Manson-Coffin's law)と言います。ここで，ｋｐとＣ_ｐは材料定数です。

有限要素法ソフトで弾塑性解析をすると相当塑性ひずみが出力されますので，(2)式を使って低サイクル疲労の寿命予測をすることができます。

同様に荷重の繰返し数が１０^４回以上において，Δε_ｅと破断繰返し数Ｎ_ｆの関係を対数グラフ上にプロットすると直線となって，その関係を次式で表すことができます。Δε_ｅ＝Δσ／Ｅなので，ΔσとＮ_ｆの関係も対数グラフで直線となり，これはＳ－Ｎ曲線になりますね。

ここで，ｋｅとＣ_ｅは材料定数です。

設計の現場では，全ひずみ範囲Δε_ｔを使うことが多く，(2)，(4)式を(1)式に代入することで次式が得られます。

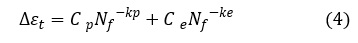
(4)式の定数Ｃ_ｐ，Ｃ_ｅ，ｋｐ，ｋｅを機械的性質から推定する式があります。以下の式です。

Langerの方法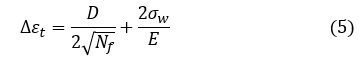

Langerの方法(5)式によると，Ｃ_ｐ，Ｃ_ｅ，ｋｐ，ｋｅは以下の値となります。

Mansonの共通こう配法

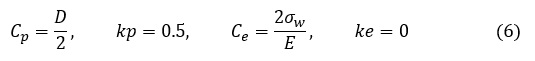
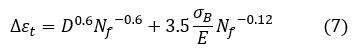
Mansonの共通こう配法(7)式によると，Ｃ_ｐ，Ｃ_ｅ，ｋｐ，ｋｅは以下の値となります。

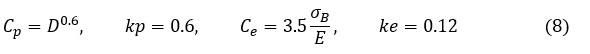
ここで，σ_ｗは両振疲労限度，σ_Ｂは引張強さ，Ｄはφを絞り[%]として次式で表す量です。

ＳＵＳ３０４材の計算例

ＳＵＳ３０４材に全ひずみ範囲Δε_ｔ＝０．０１[-]の荷重が作用する場合の破断回数Ｎ_ｆと，設計解として使われる許容破断回数Ｎ_ａｌを求めてみます。

機械的性質は，引張強さσ_Ｂ＝５２０[MPa]，両振疲労強度σ_ｗ＝１８２[MPa]（σ_ｗ＝０．３５σ_Ｂとした），ヤング率Ｅ＝１．９７×１０^５[MPa]，絞りφ＝６０[%]とします。σ_Ｂはステンレス鋼のＪＩＳ規格から，φは鋼材メーカのカタログから見つけることができます。

Langerの方法を採用し，(5)式を変形し数値を代入します。

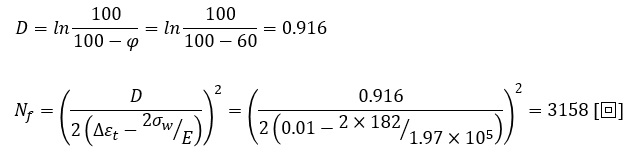
3158[回]の荷重で破壊するとの結果となりました。

許容破断回数Ｎ_ａｌを求めるには，安全率を考慮する必要があります。安全率として「荷重２倍，荷重回数２０倍の小さいほう」が妥当だと思いますので，これを採用します。

荷重２倍の破断回数として，ε_ｔ＝０．０２を上式に代入して計算しなおすと，破断回数は６３７[回]となりました。そしてマージンを含まないときの破断回数３１５８[回]の１／２０は１５７[回]となりました。小さいほうを採用して，設計で採用される許容破断回数は１５７[回]となります。

参考文献

日本機械学会，機械工学便覧　Ａ４　材料力学，(1992)