応力－ひずみ線図，延性材料と脆性材料

ＨＯＭＥ　＞　強度計算　＞　応力－ひずみ線図

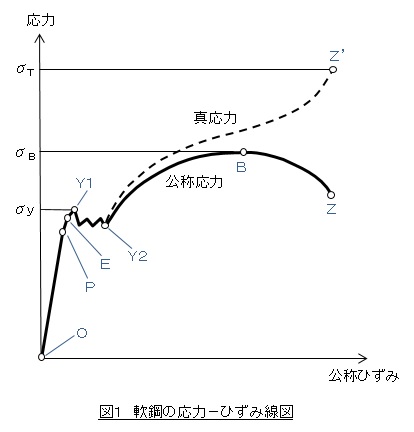
軟鋼の応力ひずみ線図

ＳＳ４００などの軟鋼を試料として引張試験をしたときに得られる応力－ひずみ線図(stress‐strain diagram)を図１に示します。横軸は公称ひずみ，縦軸は応力で実線は公称応力，破線は真応力です。

引張試験片を挙動を説明します。試験片に荷重がかかっていない状態である点Ｏから出発します。試験片を変位制御で引張っていくと，応力とひずみが比例して変形が進みます。応力（公称応力）をσｏ，ひずみ（公称ひずみ）をεｏとし，比例定数をＥで表すとσｏ＝Ｅ・εｏの関係で変形が進みます。比例定数Ｅはヤング率(Young’s modulus)ないしは縦弾性係数です。そして，これ以上引張ったら比例関係がなくなる点Ｐがやってきます。点Ｐを比例限度と言います。点Ｐで荷重を除荷したら試験片は元の形に戻ります。この性質を弾性と言います。さらに引張っていくと比例関係はなくなりますが弾性は維持した状態が少しだけあります。そして弾性を維持しきれなくなる点Ｅがやってきます。点Ｅを弾性限度と言います。Ｅ点以降は荷重を除荷したら永久変形が残ります。この性質を塑性と言います。

さらに試験片を引張って行くと，応力がＹ１点を極大値として急激に下がり，ひずみが増加しながらほぼ一定の応力が続きます。この現象を降伏と言います。図のＹ１点とＹ２点です。Ｙ１を上降伏点，Ｙ２点を下降伏点と言います。Ｙ１点の応力は試験片の形状によって変動するので，降伏応力σｙ(yield stress)に用いられるのは下降伏点の応力です¹⁾。Ｐ点，Ｅ点，Ｙ１点，Ｙ２点が近くて識別できない材料も多くあり，これらををひっくるめて降伏点(yield point)ととらえる考え方もあります。

Ｙ２点の後，ひずみの増加に伴って応力も増加します。この現象を加工硬化と言います。そして最高応力点Ｂに到達します。点Ｂの応力を引張強さσ_Ｂ(tensile strength)と言います。σ_Ｂは公称応力（荷重を変形前の断面積で割った値）であることに注意してください。Ｏ点からＢ点までは試験片の断面が一様に減少していきますが，Ｂ点以降は試験片にくびれが生じ公称応力は低下します。そしてＺ点で破断します。

一方，真応力（荷重をその時々の断面積で割った値）は，極大点Ｂを持たず増加の一途をたどります。理由はその時々の断面積が減少するからです。特にＢ点以降は試験片のくびれにより断面積が急に小さくなりますので，真応力は急上昇します。そしてＺ’点で破断します。Ｚ’点の応力を真破断応力σ_Ｔ(true stress of fracture)と言います。σ_Ｔは疲労限度線図のところで登場します。

初期長さをＬｏ，破断後の長さをＬｆとすると，伸びδは百分率[%]で表し次式で定義されます。実際の試験では，破断して残った２つの試験片を突き合わせ，予め記しておいた標点間の距離を破断後の長さＬｆとします。

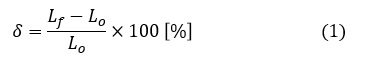
初期断面積をＡｏ，破断後の断面積をＡｆとすると，絞りφは百分率[%]で表し次式で定義されます。

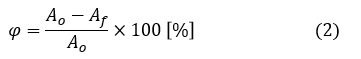
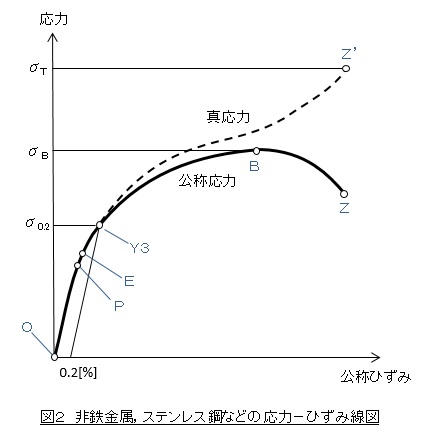
非鉄金属，ステンレス鋼，焼入れした合金鋼の応力ひずみ線図

銅やアルミなどの非鉄金属，ステンレス鋼，焼入れした合金鋼の応力－ひずみ線図を図２に示します。応力とひずみの関係が線形（比例）から非線形へ連続的に変化するところが特徴です。銅の応力－ひずみ線図を測定したことがあるのですが，比例限度ＰがＯと一致するような，つまり比例領域がないようなものでした。このように，比例限度Ｐや弾性限度Ｅを明確に定義できない場合があるので，荷重を除荷したときの永久ひずみが0.2[%]になる点Ｙ３を耐力σ_0.2(proof stress)ないしは０．２％耐力と言います。Ｙ３点以降の挙動は軟鋼の場合と同じです。

焼入れした合金鋼の場合，Ｐ点はＯ点からかなり離れたところにあります。つまり弾性領域が広いです。また耐力が高い値であることも特徴です。そして少しの塑性変形の後破断しますので，耐力と引張強さが近い値です。

延性材料と脆性材料

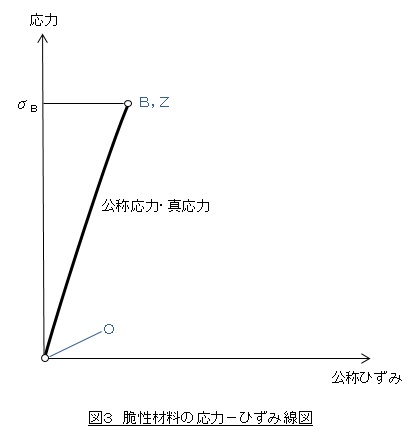
上述した応力－ひずみ特性を持つ材料を延性材料(ductile material)と言います。プラスチックも延性材料です。これに対し図３のような応力－ひずみ線図をとなる材料を脆性材料(brittle material)と言います。脆性材料では永久変形をほとんど示さずに破断します。鋳鉄，ガラス，セラミック，コンクリートなどです。

参考文献

三村，町田，基礎材料強度学，培風館，(2003)