線形破壊力学と応力拡大係数

ＨＯＭＥ　＞　強度計算　＞　応力拡大係数

適用範囲

ここでは線形破壊力学について述べます。線形破壊力学はき裂先端の塑性域の大きさが，き裂の長さに比べて十分に小さく，主として弾性論によってき裂の挙動がほぼ解析できる範囲を扱います。き裂の長さに比べて十分に小さい状態を小規模降伏（SSY small scale yielding）と言います。

式で表すと次式になります。

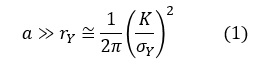
ここで，ａはき裂長さの１／２，ｒ_Ｙは塑性変形領域寸法，Ｋは後述する応力拡大係数，σ_Ｙは降伏応力です。

き裂近傍の応力

図１に示すように，長さ２ａのき裂を持つ無限に大きい平板に，十分遠いところで一様な引張応力σが作用している場合を考えます。弾性力学によれば，ｘ＞ａにおけるｘ軸上のｙ方向応力σｙは(2)式で表されます。

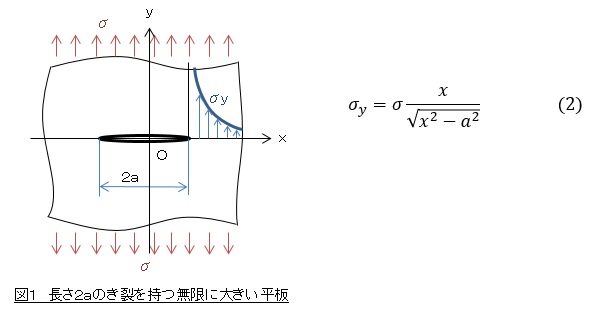
σｙはき裂先端に近づく（ｘ→ａ）につれて無限大になります。一方き裂面上（ｘ＜ａ）ではσｙ＝０です。き裂先端は応力特異点となっていて，これをき裂先端の応力特異性あるいは特異応力場と言います。

原点Ｏ’をき裂先端に移動した局所座標系を考えます。局所座標系の水平軸をｒ軸とします。これを図２に示します。

ｘ＝ａでｒ＝０となるから，ｘ＝ｒ＋ａを(2)式に代入します。σｙは(3)式で表されます。

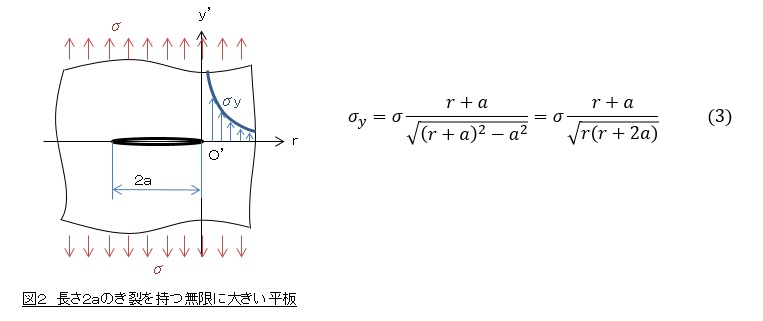
(3)式を級数展開すると次式になります。

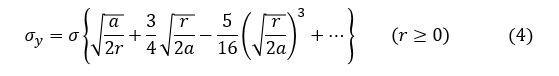
ｒ≪ａでは，(4)式の第１項がほかの項と比べて圧倒的に大きくなるため，第２項以降を無視することにすると，σｙは次式となります。

き裂近傍の応力は，１／√ｒに比例して変化する応力特異場となります。

（３）式と（５）式に数値を代入してその差を計算してみると，ｒ／ａが１／１０のとき７％程度になりますので，（５）式の近似が成立するのは，ｒがき裂長さの１／２０程度です。

応力拡大係数

(5)式を変形していきます。

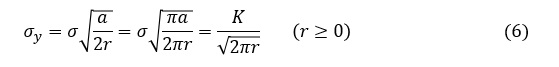
ここでＫを次式でおきました。Ｋは１／√ｒの応力特異場の比例定数のようなもので応力拡大係数（stress intensity factor）と言い，破壊力学で最も重要なパラメータです。応力拡大係数の単位はＳＩ単位系で［ＭＰａｍ^１／２］で，このサイトでは［ＭＰａ√ｍ］と表記します。

３つのき裂モード

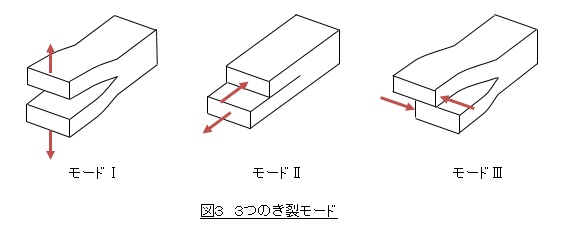
今まではき裂が開口する方向に応力が作用している場合を述べてきました。実はこの様式はモードⅠのき裂と言います。き裂の様式は３つあり，それぞれをモードⅠ，モードⅡ，モードⅢと呼び，その形態を図３に示します。

き裂近傍の応力と変位

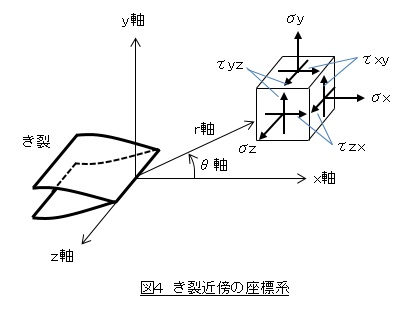
図４に示した座標系を用いて，き裂近傍の応力分布と変位分布を以下に記します。

モードⅠ

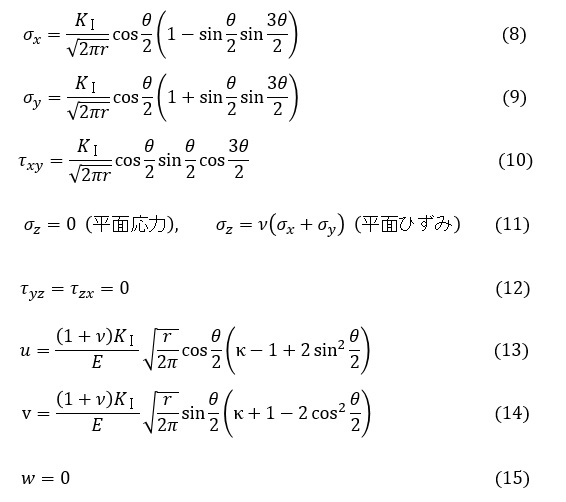
モードⅡ

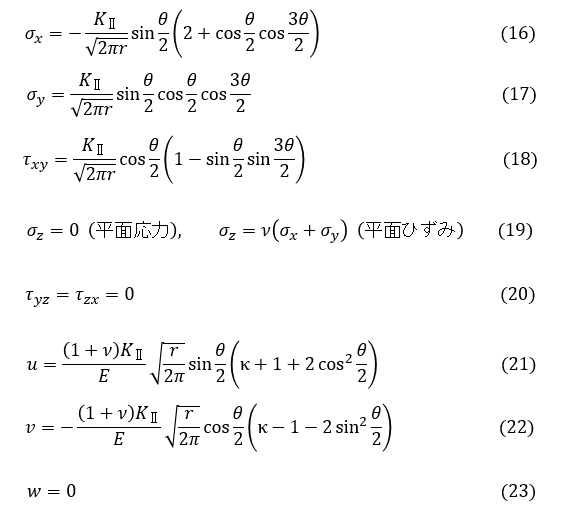
モードⅢ

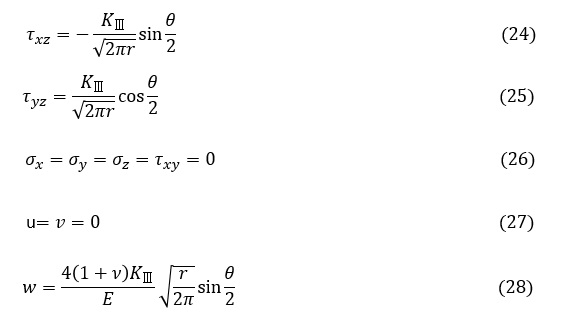
κについて

破壊力学における相似則

き裂近傍の応力分布の式（(8)，(9)式など）は，一般に次式で表すことができます。

(31)式を見ると，応力分布はＫと１／（２πｒ）^１／２とｆ_ｉｊ（θ）の積で表されています。このことは，Ｋが同じなら，部材の形状や負荷分布が変わってもき裂近傍の応力場は同じ分布になることを意味しています。同様に変位ｕ，ｖに関しても，Ｋが同じならば，き裂近傍の変位場は同じ分布になります。つまりＫが同じならば，き裂先端近傍で生じている塑性変形あるいは破壊の物理的状態が等しいといえます。

例えば，あるき裂に対してＫがＫｃ（破壊じん性値，後述）になったとき破壊したとすると，同じ材料ならば異なる形状と負荷条件であったとしてもＫがＫｃになったときに破壊します。これが，破壊力学における相似則（the similitude concept）と言います。この相似則が成立するためには，上述した小規模降伏条件が満たされていることが必要です。

疲労破壊におけるき裂進展挙動についても同様の相似則が成立し，部材の形状と負荷条件が異なっても，同じ応力拡大係数範囲ΔＫならば同じき裂進展速度ｄａ／ｄｎ［μm/cycle]となります。このことは，実験室でテストピースを使って測定した応力拡大係数とそのき裂進展挙動を，実際の構造物や機械に対して適用できることを意味します。

応力拡大係数の例

無限に大きな板の応力拡大係数のモードⅠ，モードⅡ，モードⅢの応力拡大係数は，作用する応力を図４で定義すれば，次式で表されます。

(32)式は，図５に示した無限に大きな板の応力拡大係数ですが，図６（後述します）に示すようにいろいろな形のき裂に対して応力拡大係数が求められています。応力拡大係数は一般に次式で表されます。

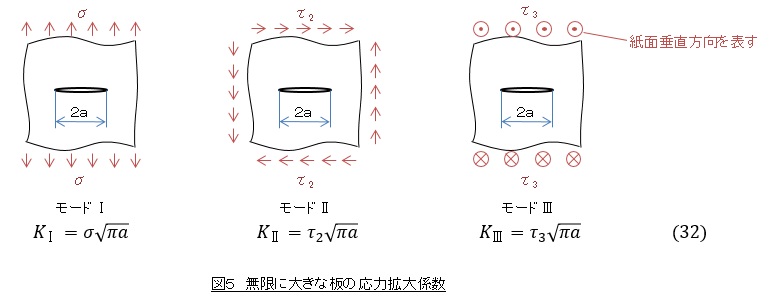
Ｆはき裂の幾何形状，有限境界あるいは負荷条件などに依存する補正係数です。

あとひとつ応力拡大係数の例を示します。図６に示すような片側にき裂がある帯板に引張荷重が作用する場合です。この式は，応力拡大係数の求め方のところで使います。

破壊じん性値

材料力学での破壊条件は次式で表されます。σ_Ｂは引張強さです。

上述したようにき裂先端の応力は無限大なので，少しでも荷重がかかれば上式を満足して破壊するとの結論になります。しかし，実際はそのようなことは起きず，小さな亀裂があっても必ずしも破壊に至るわけではありません。つまり，き裂を持つ場合には応力基準による強度評価は適用できません。そのために，破壊力学にのっとった破壊基準があります。次式で表されます。

Ｋ_Ｃはき裂が進展を開始する際の応力拡大係数の値で，破壊じん性値といいます。

応力拡大係数は，き裂が破壊するかどうかの判断に使われるだけでなく，疲労破壊によるき裂進展の有無やき裂進展速度の予測にも使われます。むしろ疲労に使われることの方が多いです。

単位換算

古い文献や海外の文献では，応力拡大係数について異なる単位を使っているのを見かけます。次式で単位換算をしてください。

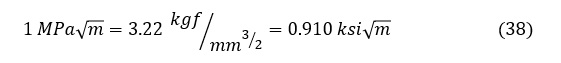
参考文献

１）日本機械学会，よく分かる破壊力学・弾性力学　講習会資料，(2013)

２）日本機械学会，機械工学便覧　基礎編　Ａ４　材料力学，丸善，(1992)

３）日本機械学会，材料力学ハンドブック＜応用編＞，(2008)

４）宮本，破壊の力学，コロナ社，(S47)