安全率

ＨＯＭＥ　＞　強度計算　＞　安全率

安全率の定義

機械や構造物に何らかの不都合を生じさせる応力を基準強さとし，設計上これ以上の応力を発生させないと決めた応力を許容応力σ_al(allowable stress)として，これらの比を安全率ｆ(safety factor)と言います。強度計算で見積もった応力（使用応力）が許容応力を上回らないように機械や構造物を設計することになります。

昔ながらの安全率

基準強さとして引張強さσ_Ｂを用い，使用応力の見積り方として公称応力とした方法が昔から行われてきました。この方法で使用する安全率を表１に示します。

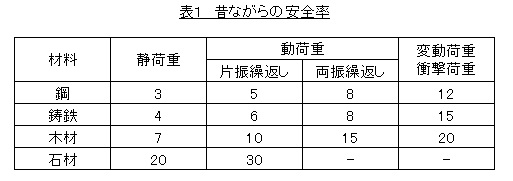
不確実な要因に加え応力集中，繰返し荷重など強度を低下させる要因など全部ひっくるめて安全率に入れています。私が勤めていた事業所では，「人命にかかわるところの安全率は１０とする。」という設計基準がありました。表１の両振繰返し荷重の安全率は８ですが，案外的を得ている数字だと思います。軟鋼の場合，引張強さと疲労限度の比は約２で，切欠係数βを２，不確実な要因に対するマージンを２とすれば，２×２×２＝８となります。

最近の安全率

応力集中による影響，繰返し荷重による影響，その他材料強度に影響を与える因子で既知のものをすべて洗い出して，これらによる影響を考慮した強度を基準強さとします。そして明確な数値として表しきれない不確実性に対するマージンを安全率ｆとします。

繰返し荷重が作用する場合を例にとって説明します。使用応力として公称応力を採用して，その許容応力σ_alは次式で表されます。

ここで

　σｗ：両振り荷重（応力比Ｒ＝－１）での疲労限度[Pa]

　ζ１：寸法効果による疲労強度の低下率[-]　０．８～１．０

　ζ２：表面状態，加工履歴，腐食環境，熱処理，使用温度などによる疲労強度の低下率[-]

　β：応力集中の影響を表す切欠き係数[-]　１．０～３．０

　ｆｍ：材料強度の不確実性を補うための安全率[-]

　ｆｓ：荷重見積りの不確実性と応力計算の近似性などに対する安全率[-]

ｆｍとｆｓの積を安全率ｆとしています。次式で表されます。

ｆｍをもう少し詳しく説明します。ｆｍは下記要因による不確実性を補うための安全率です。

• 材料の欠陥

• 化学成分，熱処理，加工など製造上の不均一性

• 標準試験試料と実物の相違

• 標準試験試料のばらつき

• 疲労限度σｗとして生存確率５０［％］の値を採用した場合，これを補う分

• β，ζ１，ζ２など材料の疲労強度に影響を与える諸因子に対する推定値の不確実さを補うための分

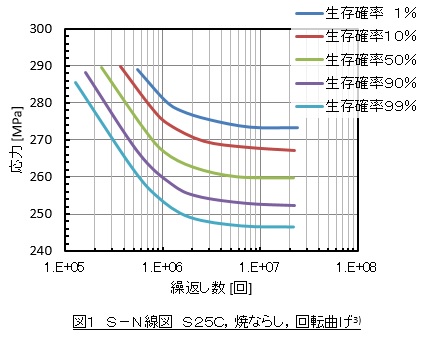
特にためらいもなく文献に載っている疲労限度σｗを使いがちですが，これらの数値のほとんどは生存確率が５０[%]での値であって，本来ならば生存確率が１００[%]に近い値での疲労限度を使うべきであることに注意が必要です。

図１は，統計処理を目的として行われた疲労試験結果の例³⁾です。生存確率５０％の疲労限度が260[MPa]，生存確率９９％の疲労限度が246[MPa]なので，生存確率５０％の疲労限度を設計計算に用いた場合，約５％のマージンを取る必要があります。

ｆｓをもう少し詳しく説明します。ｆｓは下記要因による不確実性，つまり見積った応力の不確実性を補うための安全率です。

• 部材にかかる荷重のばらつき

• 部材にかかる荷重の見積りの不確実性

• 製品寸法のばらつき

• 応力の計算過程における近似・単純化による不確実性

以上のように，安全率ｆを必要とする要因はたくさんありますが，安全率ｆは表１よりもはるかに小さい値となります。自動車や鉄道車両など，かなり確実な材料強さの試験値および正確な使用応力の測定値ならびに計算値を基に設計がなされている場合は，ｆ＝１．２～１．３程度の値が採用されています。私の場合，それほど確実な材料データを持ち合わせなかったためｆ＝２を採用していましたが，安全率ｆはそれぞれの事情に合わせて決定してください。

ＣＡＥが普及したときの取扱い

有限要素法ソフトの普及，同ソフトと計算機の性能向上から，応力集中部の応力がかなり正確に求められるようになって，使用応力として公称応力ではなく真応力（応力集中を考慮した応力）を採用できるようになりました。この結果(2)式のβを１とすることができます。有限要素法による応力計算が常態化しているところでは，この方法が主流になっていると思います。

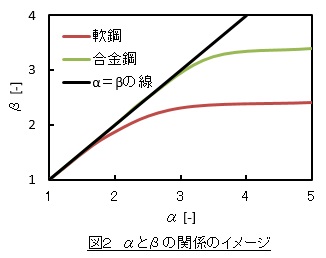
しかし，この方法は応力集中があまり激しくないとき（軟鋼の場合α≦２．５，合金鋼の場合α≦３．５のとき）最適な設計解を与えますが，応力集中が激しいとき（軟鋼の場合α＞２．５，焼入れ鋼の場合α＞３．５のとき）は，オーバースペック気味の設計解を与えることになります。図２は鋼のαとβの関係のイメージです。文献²⁾にはより詳しいデータが載っています。軟鋼の場合αが２．５以上になってもβは２．５にとどまっています。βを２．５より大きくする必要がないのです。焼入れ鋼の場合は，αが３．５以上になってもβは３．５にとどまっています。α＞２．５ないし３．５の場合，β＜αとなって，真応力を使用応力として採用すると，必要以上の大きさのβを採用することになります。(2)式に従えば，σ_alが必要以上に小さくなって，より大きな形状ないしはより高強度の材料を使ってしまうことになります。

このような場合は，使用応力として公称応力ないしはホットスポット応力を採用して，β＝２．５ないし３．５として(2)式を使って許容応力σ_alを求めて設計すると，無駄のない設計をすることができます。

参考文献

１）中山秀太郎，大学課程　材料力学，オーム社，(S53)

２）日本機械学会，金属材料　疲労強度の設計資料，Ⅰ，(S63)

３）日本機械学会，機械工学便覧　Ａ４　材料力学，(1984)