応力拡大係数の求め方

ＨＯＭＥ　＞　強度計算　＞　応力拡大係数の求め方

有限要素法を用いた応力拡大係数の計算

応力拡大係数を求めたい場合，文献に計算式が載っているのでまずこれを利用する方法を第一に考えますが，部材の形状による応力拡大係数がズバリ文献に載っていればよいのですがそうでない場合も多く，そのような場合は有限要素法を使って求めることになります。

有限要素法により応力拡大係数を求めるには，以下の方法があります。¹⁾

• 直接法：直接変位法，直接応力法
• エネルギ法：全エネルギ法，ＶＣＥ法，Ｊ積分法
• 重ね合わせ法：山本の方法，特異要素（Ｂａｒｓｏｕｍの特異要素，Ａｋｉｎの特異要素）の使用など

ハイエンドの有限要素法ソフトでは，応力拡大係数Ｋ，エネルギ開放率Ｇ，Ｊ積分値を直接求める機能がありますので，これを使う選択肢が現実的です。

ここでは，Ｋ，Ｇ，Ｊを求める機能のない普通の有限要素法ソフトで，直接変位法を用いて応力拡大係数を求める方法を説明します。

直接変位法

変位法による有限要素法では，変位が直接求まり応力は変位を微分したものであるため，変位の方が精度が高いです。よって，直接応力法ではなく直接変位法を使います。直接変位法を使ってモードⅠ（平面応力状態）の応力拡大係数Ｋ_Ⅰを求める方法を説明します。

図１のような座標系を設定したときのモードⅠのｙ方向変位ｖは，応力拡大係数のページで述べたように(1)式で表されます。

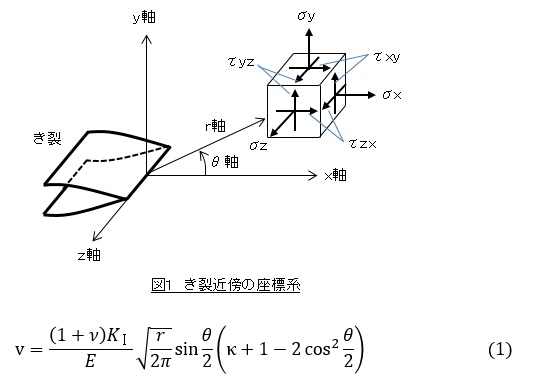
ここでκは次式で表されます。

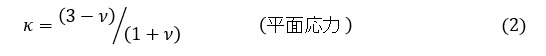
有限要素法でＫを求めるときは，き裂の開口側の変位を使います。ν＝0.3[-]として(1)式にκとθ＝180[°]を代入すると，き裂開口部の変位ｖは次式となります。

図２に，き裂が開口するような荷重が作用したときのき裂の形状を示します。θ＝180[°]なのでｒ軸は－ｘ方向を向きます。き裂の形状ｖ（ｒ）は√ｒに比例した形になります。ｒにおける変位ｖ（ｒ）を使って応力拡大け数Ｋ_Ⅰを求めます。

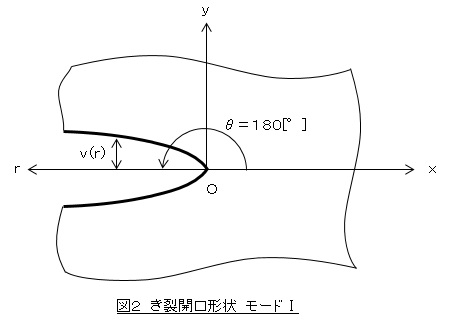
(3)式を変形します。

有限要素法で解析したいき裂をモデリングし荷重条件を与えて解析して，き裂部近傍節点の節点座標とｙ方向変位ｖをテキスト出力します。節点座標からｒ座標を求め，ｒ値（単位は[m]）とｙ方向変位ｖ（単位は[m]）を(4)式に代入してＫ_Ⅰを求めます。このときヤング率の単位を[MPa]としておきます。鉄なら２×１０^５[MPa]ですね。き裂線上の節点数をｎとすればｒ値とＫ_Ⅰ値はｎ組あります。次に図３に示すように横軸をｒ値，縦軸をＫ_Ⅰ値（単位は[MPa√m]）としてグラフ用紙にプロットします。と言っても今はエクセルの散布図ですね。

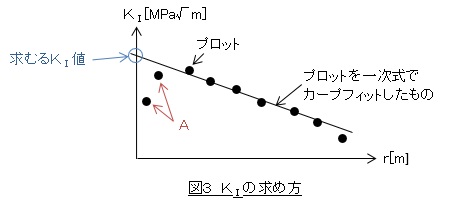
そして，プロット群を使って外挿してｒ＝０[m]におけるＫ_Ⅰ値を求めます。具体的には，プロットを１次式でカーブフィットして，その式の縦軸切片がＫ_Ⅰ値となります。このときｒ＝０[m]近傍で，カーブフィットした式から離れるプロット（図３のＡ）が現れますが，これらは無視します。

以上が直接変位法によるＫ_Ⅰの求め方です。同様の手順でＫ_Ⅱ，Ｋ_Ⅲも求めることができます。

計算例

図４のようなき裂のＫ_Ⅰを実際に有限要素法を使って求めてみましょう。最初に断っておきますが，応力拡大係数の計算では長さの単位は[m]，応力の単位は[Pa]で行ってください。そして④式の計算の段階のときだけヤング率の単位を[MPa]にしてください。そうすればＫ_Ⅰの単位は[MPa√m]になります。

図４の問題は答がありまして，次式で表す近似式で応力拡大係数を求めることができます。

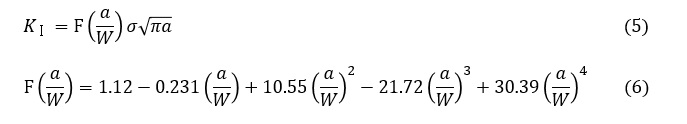
応力拡大係数は6.63[MPa√m]です。それでは，有限要素法を使ってＫ_Ⅰを求めてみましょう。

図５のようなモデルを作ります。解析対象は上下対称なので上半分だけモデル化した１／２対称モデルで計算します。そしてき裂先端付近は特別に小さな要素分割をするため，ボリューム分割をしております。

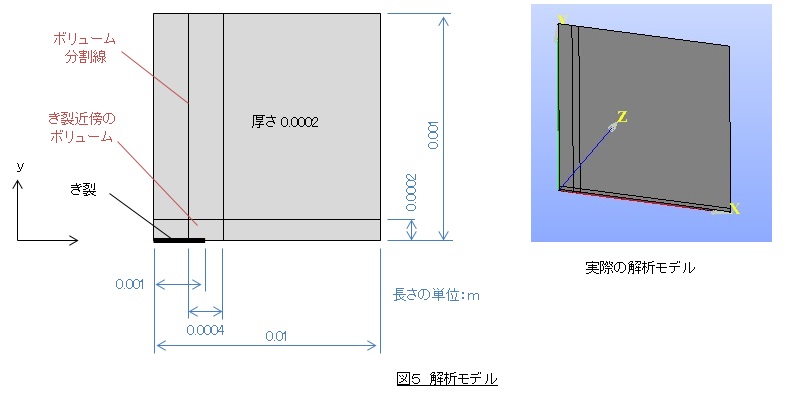
三次元ＣＡＤでモデリングして，それを有限要素法ソフトに読込んで解析するような方を説明の対象としておりますので，解析モデルは薄い板の三次元モデルとしました。二次元解析ができる方は平面応力問題として取組んでください。

次に，図６のような境界条件を設定します。普通，要素分割の後に境界条件を設定しますが，便宜上ここで説明しておきます。

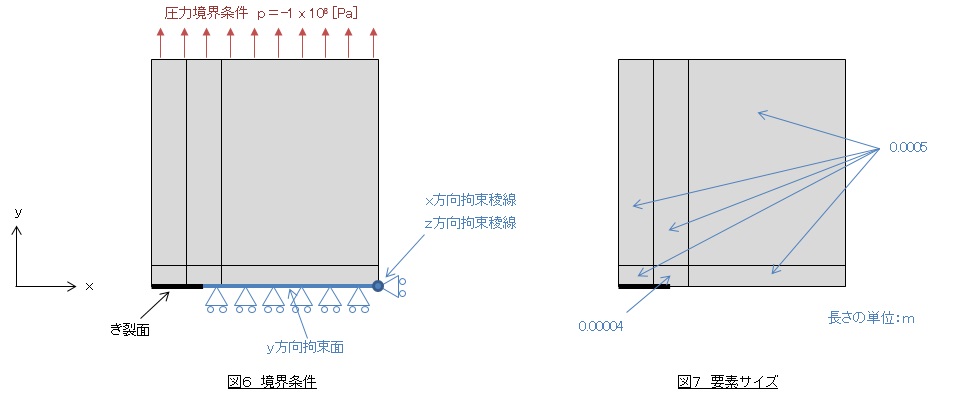
要素分割では，き裂近傍のボリュームを細かく分割します。図７に分割する要素サイズを示します。実際に分割した要素を図８に示します。

応力拡大係数のページで述べたように，(1)式による近似が成立するのはき裂先端からき裂長さの１／１０の距離の範囲です。よって要素分割はき裂長さの１／１０の距離のところが細かくなるようにします。

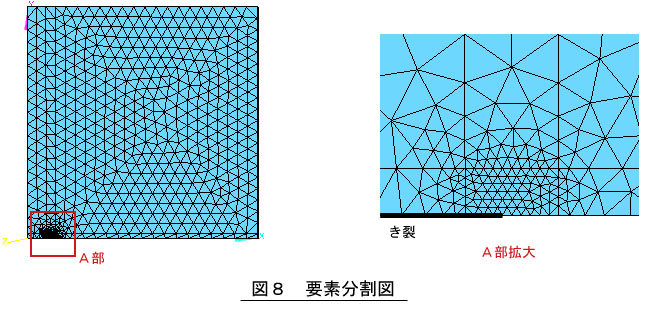
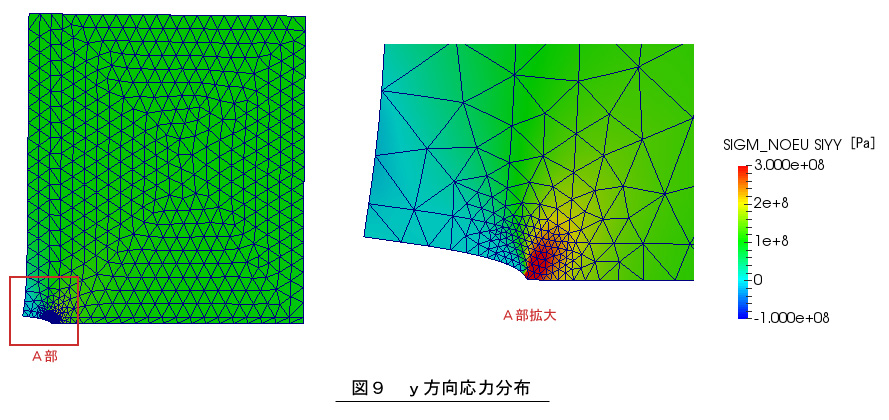
図９に解析結果のうちのｙ方向応力分布を示します。き裂開口部のｙ方向変位が√ｒに比例した量であることがわかります。

き裂面上の節点について，節点座標とｙ方向変位をテキスト出力してエクセルに読込みます。節点のｘ座標値からｒ座標を計算し，(4)式からＫ_Ⅰを計算し，それをプロットしたもの（◆青色プロット）を図１０に示します。そしてプロットを１次式でカーブフィットした線を赤色の線で示します。カーブフィットした線の縦軸切片が求むるモードⅠの応力拡大係数Ｋ_Ⅰです。

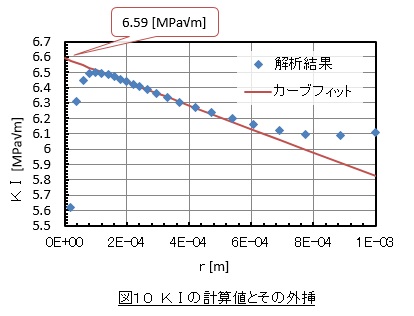
有限要素法によるＫ_Ⅰ値は6.59[MPa√m]となりました。(5)，(6)式による値は6.63[MPa√m]ですので0.6[%]の差です。なかなか良い一致をみました。

参考文献

日本機械学会，計算力学ハンドバック，丸善，(1998)