き裂進展速度，パリス則，下限界応力拡大係数範囲ΔＫ_ｔｈ

ＨＯＭＥ　＞　強度計算　＞　き裂進展速度，パリス則，下限界応力拡大係数範囲Δｋ_ｔｈ

き裂の発生と進展

疲労破壊はき裂の発生と進展という二つの過程からなります。しかしながら，両者の境界を定めることは実際上困難なため金属材料については，き裂発生段階を含めてすべり帯に沿う初期き裂進展過程を第１段階，その後の巨視的には最大引張応力の作用面に沿うき裂進展過程を第２段階と呼んで，疲労破壊の進展過程を区別した取扱いをします。このうち，破壊力学的取扱いが有効なのは第２段階のき裂進展過程に対してであります。

ここで，応力拡大係数範囲ΔＫ（stress intensity factor range）を次式で定義します。

Ｋ_ｍａｘは繰返し荷重の１サイクル当たりの応力拡大係数の最大値，Ｋ_ｍｉｎは１サイクル当たりの応力拡大係数の最小値です。

ΔＫが大きいとき裂がどんどん進展し，ΔＫが小さいとき裂の進展量も小さくなります。今，荷重１サイクル当たりのき裂進展量をｄａ／ｄｎと表記します。ｄａ／ｄｎをき裂進展速度（fatigue crack propagation rate）と呼び，その単位は［μｍ／ｃｙｃｌｅ］となります。上述した第２段階において，ｄａ／ｄｎとΔＫの関係を両対数グラフで表すと図１のようになります。

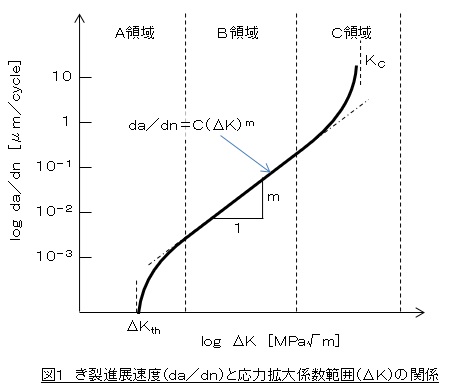
図１に示したようにき裂進展特性はＡ，Ｂ，Ｃの３領域に分けられます。領域Ａから説明します。

下限界応力拡大係数範囲ΔＫ_ｔｈ

図１の領域Ａでは，ΔＫを小さくしていくとき裂進展速度（ｄａ／ｄｎ）が急に小さくなっていき，ΔＫ＝ΔＫ_ｔｈのところでき裂の進展は観測できなくなります。このΔＫ_ｔｈを下限界応力拡大係数範囲（threshold value of stress intensity factor range）と言い，多くの鋼について合金成分や熱処理条件によらず，３～８［ＭＰａ√ｍ］程度の値となります。応力比（Ｒ＝σ_ｍｉｎ／σ_ｍａｘ＝Ｋ_ｍｉｎ／Ｋ_ｍａｘ）が小さいほどΔＫ_ｔｈは大きな値となり，Ｒが大きいほどΔＫ_ｔｈは小さくなります。

設計における強度計算ではΔＫ_ｔｈが重宝します。有限要素法ソフトでΔＫを求めておき，それとΔＫ_ｔｈを比較することで疲労破壊の有無を予測することができます。計算で求めたΔＫが，ΔＫ_ｔｈより小さいと疲労破壊はしないと判断できます。高い応力比（Ｒ≧０．５）を想定して，鋼（オーステナイト系ステンレス鋼を含む）の場合ΔＫ_ｔｈ＝２．０［ＭＰａ√ｍ］，アルミニウム合金の場合０．７［ＭＰａ√ｍ］としておけば問題ないと思います¹⁾。他の金属では，ヤング率ＥとΔＫ_ｔｈの間には次式で示す関係²⁾（Ｒ＝０．８）がありますので，ヤング率さえわかればΔＫ_ｔｈが求まります。

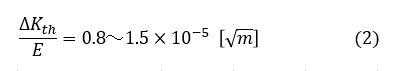
パリス則

図１のＢ領域では，き裂はき裂先端のすべり面分離によるストライエーション（striation）形成が支配的な機構となって進展します。そして，両対数グラフにおいて，き裂進展速度（ｄａ／ｄｎ）と応力拡大係数範囲（ΔＫ）の関係は傾きがｍの直線となって，次式で表すことができます。この関係をパリス則（Paris low）といいます。

ここでＣとｍは材料定数です。

(3)式の代りに次式を使うとより広い領域について適用可能となります³⁾。

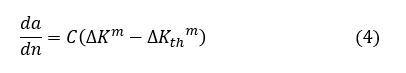
領域Ｃについて

領域Ｃでは，ΔＫの増大に伴って静的破壊と同様な微視破壊モード（へき開，粒界割れ，微小空洞合体）が介在して，き裂進展速度が著しく加速され，ついにはΔＫ＝Ｋ_Ｃ（破壊じん性値）になったところで，１回の荷重サイクルで破断してしまいます。

以上がき裂進展速度と応力拡大係数範囲の関係です。

参考文献

１）A.F. Hobbacher, Recommendations for Fatigue Design of Welded Joints and Components, IIW Collection, DOI 10.1007/978-3-319-23757-2_7

２）宇佐美，志田，破壊力学による溶接継手の疲労強度評価，圧力技術，20 巻　2号，(1982)

３）（社）日本鋼構造協会，鋼構造物の疲労設計指針・同解説，技報堂出版，(2004)

４）日本機械学会，機械工学便覧　基礎編　Ａ４　材料力学，丸善，(1992)