線形累積損傷則

線形累積損傷則は，応力振幅が単一ではなく図１のように複数あったり，応力が時間の経過とともにランダムに変動する場合の疲労破壊の有無を予測する方法です。

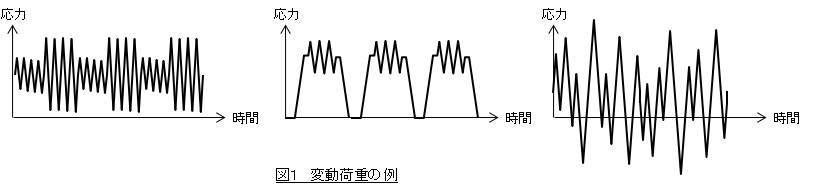
応力振幅がσ_ｗ１，σ_ｗ２，σ_ｗ３，．．．の荷重がｎ_１回，ｎ_２回，ｎ_３回，．．．作用しているとします。損傷度Ｄを次式で表し，Ｄが１より小さければ疲労破壊し，Ｄが１より大きければ疲労破壊しないと判断します。

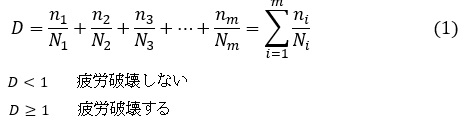
ここで，Ｎ_１回，Ｎ_２回，Ｎ_３回，．．．は応力振幅σ_ｗ１，σ_ｗ２，σ_ｗ３，．．．のときの寿命（荷重回数）で，図２のようにＳ－Ｎ線図から求めます。

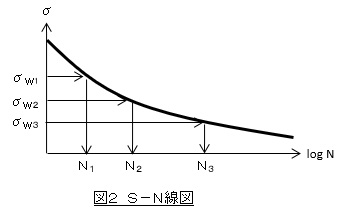
損傷度Ｄの境界値を１としましたが，いくつかの論文では１より小さい値を提案しています。しかし，境界値を１として後述する安全率を取ることで対処すればよいと思います。

マイナー則

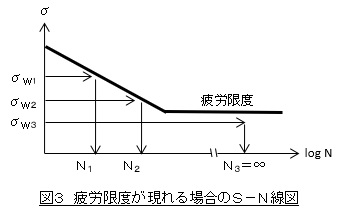
アルミニウム合金やステンレス鋼など鉄鋼材料以外の材料は図２のような特性を示しますが，鉄鋼材料だけは図３に示すような疲労限度が現れます。疲労限度が現れる場合，疲労限度以下の応力振幅（σ_ｗ３）に対する寿命（Ｎ_３）は無限大となり，損傷度をゼロとします。このような方法をマイナー則と言います。

しかし，疲労限度以下の応力振幅によっても材料はダメージを受けていることが知られており，事項で述べる修正マイナー則を使うべきだと考えています。

修正マイナー則

図４に示すように，疲労限度が現れる領域においてＳ－Ｎ曲線の傾斜部分を延長して疲労寿命Ｎ_ｉを求める方法が修正マイナー則です。図の場合，Ｎ_３は無限大ではなく有限のある値を持つことになります。

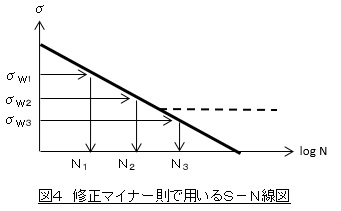
Ｓ－Ｎ曲線の表し方

図２～図４は，横軸を対数とし縦軸を対数ではなく実数として表しています。縦軸を実数とした場合，Ｓ－Ｎ曲線が図３，図４のように直線となることはまれで，多くの場合は図２のように曲線となります。

そこで縦軸も対数で表すとＳ－Ｎ曲線が直線に近づきます。式で表すと次式になり，図で表すと図５のようになります。この直線を求めるにはＳ－Ｎ曲線を(2)式でカーブフィットします。つまりＳ－Ｎ曲線のデータと(2)式による値の差が最小になるように材料定数Ｃとｍを求めます。カーブフィットの方法は後述する計算例で詳しく説明します。

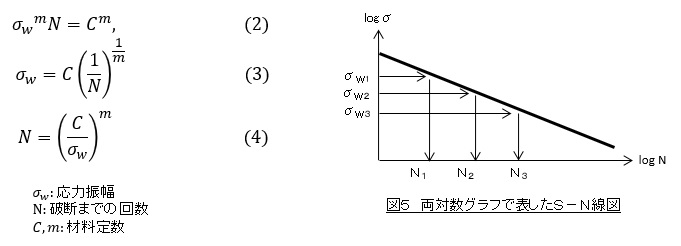
平均応力を考慮したＳ－Ｎ曲線の表し方

通常文献に載っているＳ－Ｎ曲線は両振の応力振幅での値です。つまり平均応力がゼロでの値です。一方，同じ応力振幅でも平均応力がある場合の疲労寿命は，平均応力がない場合（両振応力振幅）の疲労寿命より短くなります。Ｓ－Ｎ曲線にこの短くなった分を考慮する必要があります。私は以下の手順で行っています。

　①修正グッドマン線図を作成します。（図６）

　②平均応力がσ_ｍのときの応力振幅σ_ｗを読取ります。

　③平均応力がσ_ｍのときの応力振幅σ_ｗと平均応力がゼロのときの応力振幅σ_ｗｏとの比γ（ガンマ）を次式で求めます。γは１より小さい値になります。

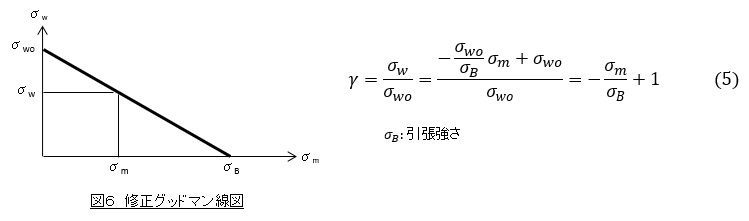
　④Ｓ－Ｎ曲線をγ倍します。Ｓ－Ｎ曲線を両対数グラフで表している場合は，図７に示すようにＳ－Ｎ曲線を下へ平行移動することになります。

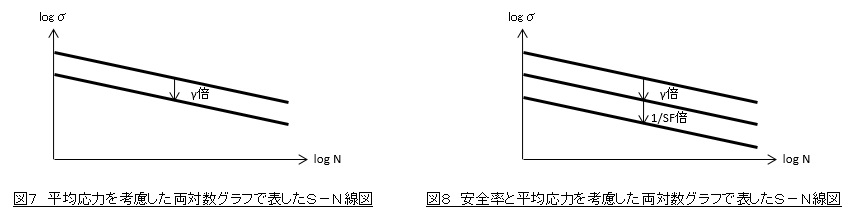
安全率と平均応力を考慮したＳ－Ｎ曲線の表し方

安全率ＳＦを考慮する場合はＳ－Ｎ曲線を１／ＳＦ倍します。Ｓ－Ｎ曲線を両対数グラフで表している場合は，図８に示すようにＳ－Ｎ曲線を下へ平行移動することになります。

式で表すと次式になります。

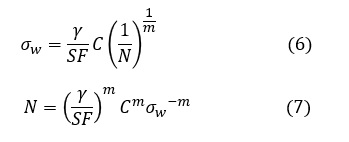
損傷度Ｄが１／２だからと言って安全率が２あるという判断は間違っています。(6)，(7)式を使った場合，安全率が２になるときのＤは１０のマイナス数乗となります。

計算例

荷重条件

アルミニウム材（A5052）に，下表に示すような繰返し荷重が同時に作用するときに疲労破壊するかどうかを予測してみましょう。アルミニウム材のＳ－Ｎ線図を図９であるとします。

Ｓ－Ｎ曲線のカーブフィット

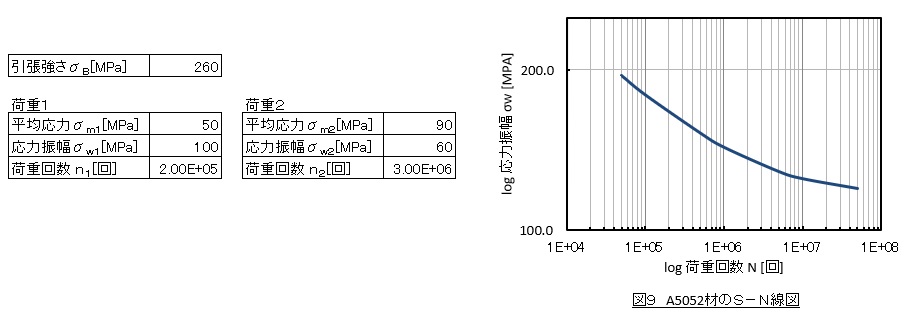
後の作業を簡単にするためにＳ－Ｎ曲線を(2)式でカーブフィットします。

要するにＳ－Ｎ曲線と(2)式が一致するような材料定数Ｃとｍを求めればよいのです。ここではエクセルのソルバー機能を使ってＣとｍを求めます。

エクセルでソルバー機能を使えるようにする準備

エクセルをインストールしただけではソルバー機能は使えません。ソルバー機能をインストールする必要があります。下記手順でインストールしてみてください。

　①エクセルのファイルをクリックする。

　②一番下のオプションをクリックする。

　③下の方のアドインをクリックする。

　④下の方の「設定(G)...」ボタンを押す。

　⑤図１０に示すようにソルバーアドインのところのチェックを入れて，「ＯＫ」ボタンを押す。

　⑥図１１のようにソルバー機能が使えるようになります。

Ｓ－Ｎ曲線のカーブフィット

図１２にＣとｍを求めるエクセルシートを示します。カーブフィットの手順を以下に記します。

　①Ｃとｍに適当な数値を入力しておきます。Ｃ＝200，ｍ＝3がおすすめです。

　②Ｓ－Ｎ曲線から読取った「荷重回数 [回]」と「Ｓ－Ｎ曲線から読取ったσ_ｗ[MPa]」の数値を入力します。

　③「カーブフィットしたσ_ｗ[MPa]」の列に(3)式を代入します。

　④「Ｓ－Ｎ曲線から読取ったσ_ｗ[MPa]」と「カーブフィットしたσ_ｗ[MPa]」の差の自乗を求める計算式を「差の自乗」の列に入力します。

　⑤「差の自乗」の合計を求める計算式を入力します。

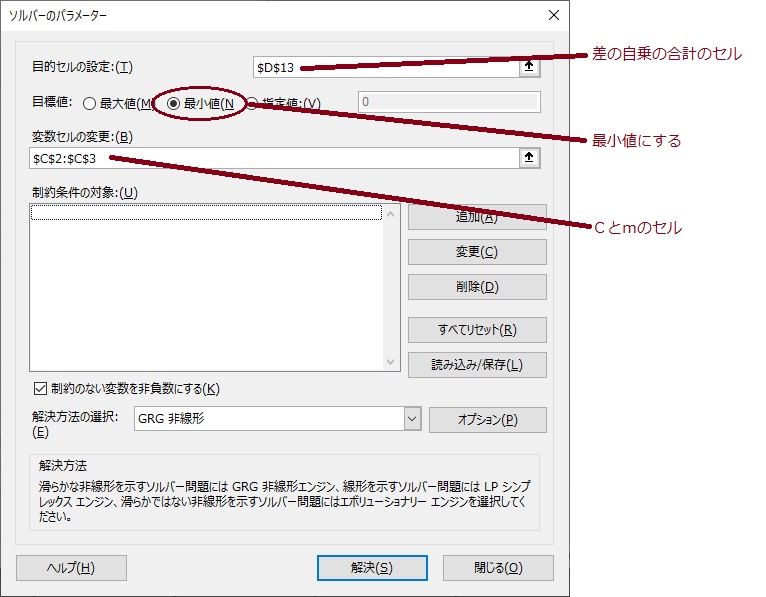
　⑥ソルバー機能を使って，「差の自乗」の合計が最小となるようなＣとｍを求めます。ソルバーの画面を図１３に示します。図１２のエクセルシートは，ここからダウンロードできます。

Ｃとｍは図１２に示すような値とになりました。

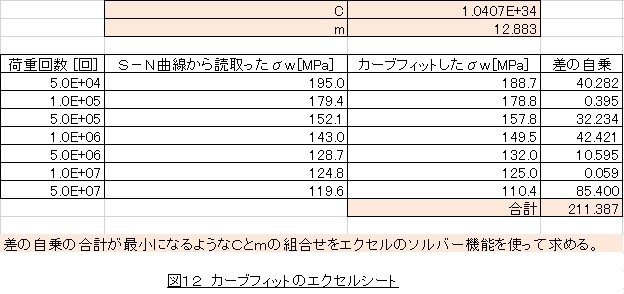
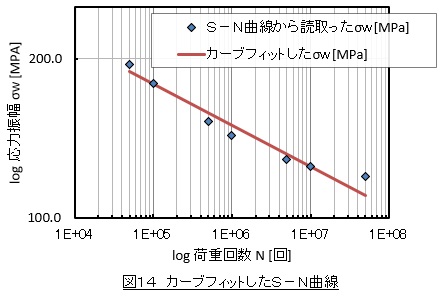
求まったＣ，ｍと(3)式を使ってカーブフィットしました。これを図１４の赤線で示します。

荷重１の損傷度ｎ_１／Ｎ_１の計算

損傷度Ｄの第１項（(1)式の第１項）を求めます。

平均応力があるため図１４のＳ－Ｎ曲線をγ（ガンマ）倍する必要があります。γを求めるために修正グッドマン線図を作成します。

修正グッドマン線図のＸ軸切片は引張強さσ_Ｂで，Ｙ軸切片は両振の疲労強度σ_ｗｏです。両振の疲労強度σ_ｗｏは，図１４で荷重回数がｎ_１のときの応力振幅とします。図１４から読取ってもいいのですがここでは(3)式を使いましょう。

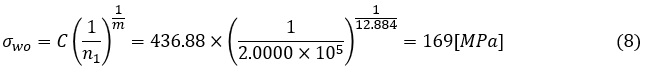
σ_ｗｏ＝169[MPa]となりましたので修正グッドマン線図を作成できます。これを図１５に示します。平均応力σ_ｍ１＝50[MPa]のときの応力振幅σ_ｗは図から読取って137[MPa]となりました。よってγは137[MPa]／169[MPa]＝0.808[-]となりました。

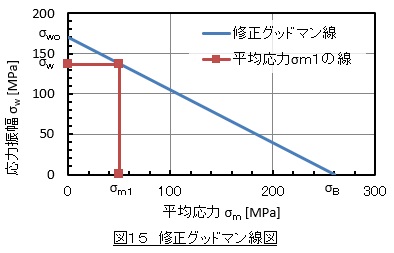
γは修正グッドマン線図を作図しなくても(5)式を使ってσ_ｍ１とσ_Ｂから求まります。次式で示します。

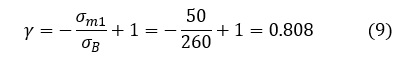
Ｓ－Ｎ曲線をγ倍したものを図１６に示します。Ｓ－Ｎ曲線は(3)式で表しているので，データのないＮ＝10¹⁴[回]まで延長します。そして，応力振幅σ_ｗ１（100[MPa]）のときの寿命Ｎ_１をＳ－Ｎ線図から読取りましょう。Ｎ_１＝1.14 x 10⁷回となりました。

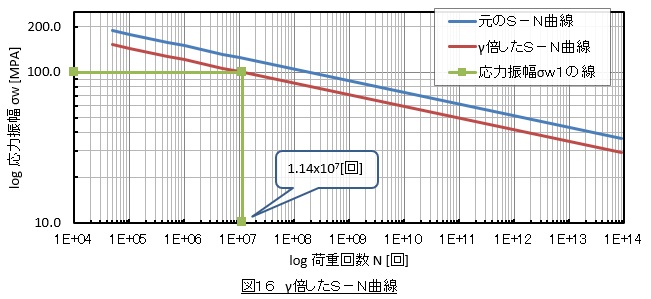
Ｓ－Ｎ曲線を作成くなくても(7)式で寿命Ｎ_１が求まります。次式です。課題は疲労破壊の有無の判定なので安全率を１[-]としました。

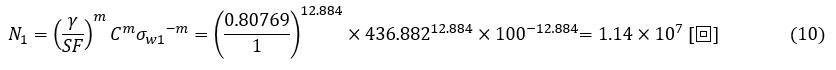
損傷度Ｄの第１項は次式の値となります。

荷重２の損傷度ｎ_２／Ｎ_２の計算

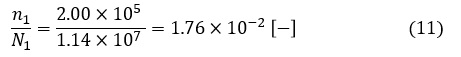
同様の手順で損傷度Ｄの第２項（(1)式の第２項）を求めます。

(5)式からγは次式で求まります。

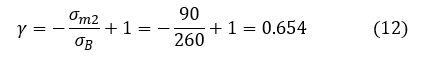
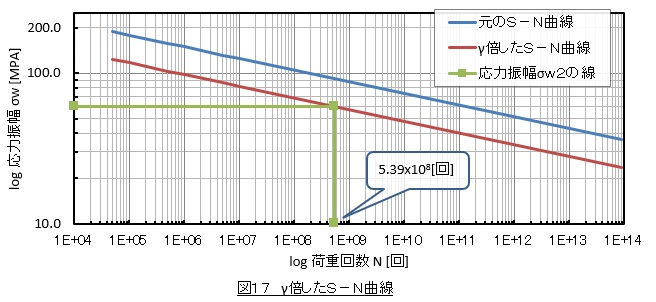
(7)式があるのでＳ－Ｎ線図を作成する必要はないのですが，一応書いておきましょう。図１７に示します。応力振幅σ_ｗ２（60[MPa]）のときの寿命Ｎ_２をＳ－Ｎ線図から読取るとＮ_２＝5.39 x 10⁸回となりました。

Ｓ－Ｎ曲線を作成くなくても(7)式で寿命Ｎ_１が求まります。次式です。ここでも安全率は１[-]としました。

損傷度Ｄの第２項は次式の値となります。

疲労破壊の有無の判定

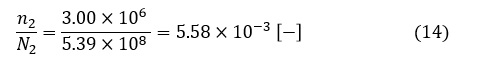
(11)式と(14)式の値を(1)式に代入すると損傷度Ｄは次式の値となります。

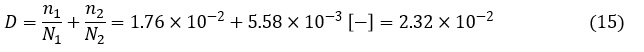
損傷度Ｄが１より小さいため，疲労破壊しないと判定されます。