応力

ＨＯＭＥ　＞　材料力学　＞　応力

応力（垂直応力）

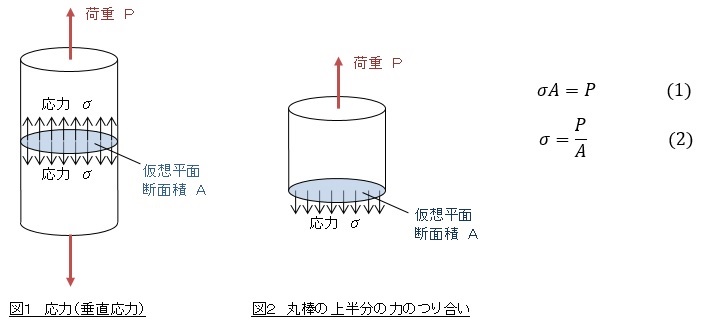
図１に示すような丸棒に引張荷重Ｐが作用し，かつ静止している場合を考えます。丸棒の中に仮想平面を想定しましょう。 仮想平面に働く単位面積当たりの力を垂直応力σ(normal stress)と呼びます。 ほとんどの場合この垂直応力を単に応力σ(stress)と呼んでいます。 図２のように丸棒を仮想平面で切断しそれに作用する力を考えます。 丸棒は静止しているため力のつり合いが成立します。つり合いを式で表すと式(1)のようになります。 式(1)を変形して式(2)のようになって，応力σは荷重Ｐを断面積Ａで割ることによって求めます。

せん断応力

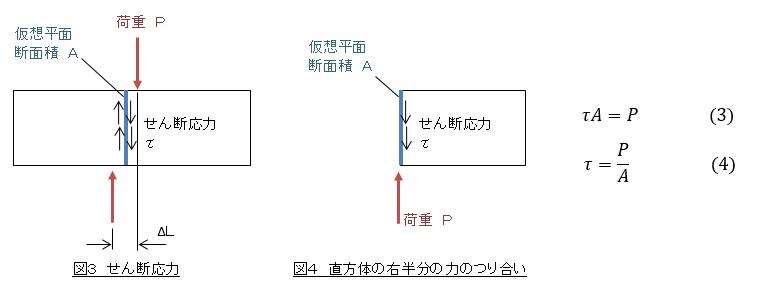
図３に示すような，直方体にせん断荷重Ｐが作用し静止している場合を考えます。 ここでせん断荷重Ｐの間隔ΔＬはゼロではないが非常に小さな値であるとします。 直方体の中に仮想平面を想定しましょう。 仮想平面に働く単位面積当たりの力をせん断応力τ(shearing stress)と呼びます。 図４のように直方体を仮想平面で切断しそれに作用する力を考えます。 直方体は静止しているため力のつり合いが成立します。 つり合いを式で表すと式(3)のようになります。 式(3)を変形して式(4)のようになって，せん断応力τは荷重Ｐを断面積Ａで割ることによって求めます。

応力の厳密な定義

上述した説明では，仮想平面内の応力は位置に関係なく一定値と仮定していました。 しかし実際の応力は図５に示すように場所ごとに異なる値を持ち，座標(x,y,z)の関数となります。

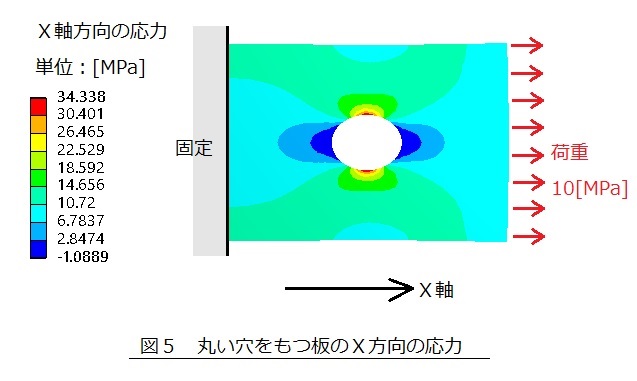
今，図６に示すような物体が下の方で固定されており，上の方で荷重Ｐが作用しているとします。物体を仮想平面で切断し仮想平面上のある点をＰ（x,y,z）とし，Ｐを中心とした微小な面を考えます。仮想平面の法線ベクトルをnとします。太字はベクトルを表しています。そして，微小な面の面積をΔｓとします。切断した仮想平面内の微小なΔｓには力ΔＴが作用しています。

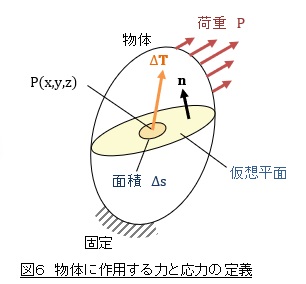
ΔＴをΔｓで除した値ｔは，応力と同じ次元を持つベクトル量となります。Δｓを限りなくゼロに近づけたとき，「①ｔはある値に収束すること，②面積がゼロなのでモーメントの腕の長さもゼロで，力のつり合いを考えるときにモーメントのことは考えなくてもよい。」と言えます。Cauchyはこのように考えたそうです。これを「Cauchyの応力原理」と言います。このときのｔを表面力ベクトル（traction vector）と言い，面Δｓではなく点Ｐ固有の値となります。

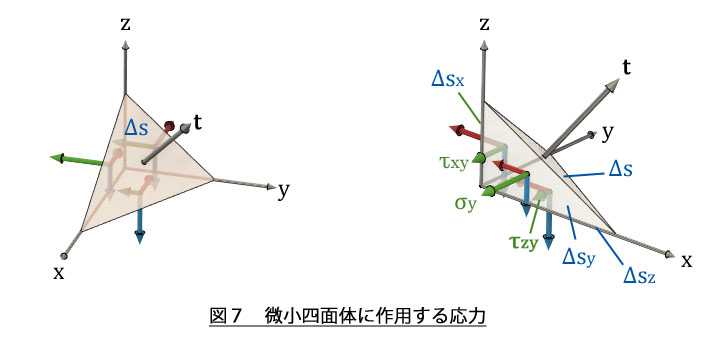
ｔは，物体を仮想平面で切断したときの方向，つまり，法線ベクトルｎの方向によって変化します。普段，x,y,z座標系を使っているので，x,y,z座標系でｔを表現しましょう。図７はΔｓ近傍の領域を，ｘ軸に垂直な面，ｙ軸に垂直な面，ｚ軸に垂直な面でカットした四面体を表しています。四面体の斜めの面がΔｓ，ｘ軸に垂直な面の面積がΔｓ_ｘ，ｙ軸に垂直な面の面積がΔｓ_ｙ，ｘ軸に垂直な面の面積がΔｓ_ｚです。

この四面体に作用する力についてｙ方向の力のつり合いを考えてみましょう。ｘ軸に垂直な面Δｓ_ｘには，ｘ軸方向の応力σ_ｘと，ｙ方向のせん断応力τ_ｘｙ，ｚ方向のせん断応力τ_ｘｚが作用しています。ｙ軸に垂直な面Δｓ_ｙには，ｙ軸方向の応力σ_ｙと，ｘ方向のせん断応力τ_ｙｘ，ｚ方向のせん断応力τ_ｙｚが作用しています。ｚ軸に垂直な面Δｓ_ｚには，ｚ軸方向の応力σ_ｚと，ｘ方向のせん断応力τ_ｚｘ，ｙ方向のせん断応力τ_ｚｙが作用しています。図にはｙ方向に関係する応力τ_ｘｙ，σ_ｙ，τ_ｚｙだけ緑色で示しています。

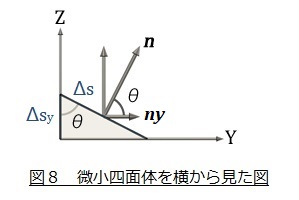
次に，Ｘ軸に垂直な面Δｓ_ｘ，Ｙ軸に垂直な面Δｓ_ｙ ，Ｚ軸に垂直な面Δｓ_ｚとΔｓの関係を調べましょう。図８は微小な四面体をＸ軸から見た図です，ベクトルｎ はΔｓ面の法線ベクトルで大きさを1とします。微小四面体のＹ軸に垂直な面Δｓ_ｙの面積はΔｓ・ｃｏｓθ ですね。また表面の法線ベクトルのＹ方向成分ｎ_ｙは｜ｎ｜ ｃｏｓθなのですが，｜ｎ｜ ＝１なので，ｎｙ ＝ｃｏｓθです。よって，Δｓ_ｙの面積はΔｓ・ｎ_ｙとなります。ここの所，本当は３次元的に説明しなければならないのですが，わかりやすさを優先して２次元で説明しました。(5)式です。

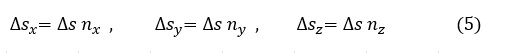
力の釣り合い式です。表面力ベクトルｔの Ｙ方向成分ｔ_ｙ は物性内部の応力と釣り合っているので次式が成立します。

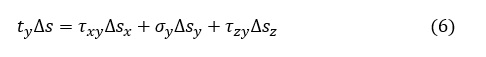
(6)式に(5)式を代入します。

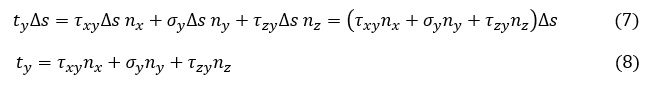
同様にして以下の３式が成立します。

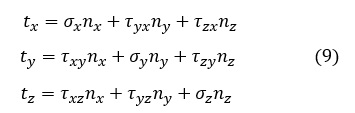
表面力ベクトルｔ，法線ベクトルｎを使って，上式を以下にように表します。

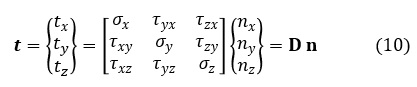
上式をCaychyの式と言います。3行3列の正方行列Ｄは，任意の切断面の大きさ１の法線ベクトルから，その切断面に作用している表面力ベクトルｔを求めるための線形変換作用素ということができます。

また，Ｄは点Ｐの応力状態を表現しているテンソル量となります。

点Ｐは点であって微小六面体ではないのですが，六面体を使って応力テンソルの各成分を図９に示します。六面体に９種類１８個の応力が作用して釣り合っています。六面体のモーメントもつり合っているはずなので次式が成立します。

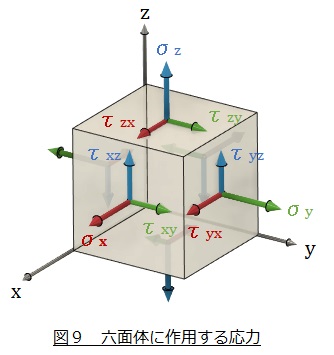
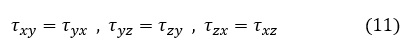
９個の応力成分が６個になりました。Ｐ点の応力を決定づける応力テンソルは以下のように３行３列の対称マトリクスで表現されます。以上が応力の定義です。

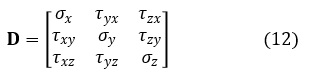
応力の符号

大事な約束事があります。 図１のように丸棒が引張られているときの応力を引張応力(tensile stress)といい， その符号はプラスです。反対に圧縮応力(compressive stress)の符号はマイナスです。 ＣＡＥソフト（有限要素法ソフト）が出力する応力の符号も同じルールで，引張応力はプラス値，圧縮応力は マイナス値です。

応力の単位

応力は単位面積当たりの力なので圧力の単位と同じで，ＳＩ単位系での応力の単位は ［Ｎ／ｍ^２］です。パスカル［Ｐａ］と表記します。 他には［Ｎ／ｍｍ^２］，［ＭＰａ］，［ｋｇｆ／ｍｍ^２］なども使われます。 有限要素法で計算するとき，荷重の単位をニュートン［Ｎ］や［Ｐａ］で入力し三次元モデルを［ｍ］で作成した場合， 解析結果の応力の単位は［Ｐａ］となります。 荷重をニュートン［Ｎ］や［ＭＰａ］で入力し三次元モデルを［ｍｍ］で作成した場合，応力の単位は［ＭＰａ］となります。 有限要素法で計算した結果を報告書にまとめるときは［ＭＰａ］を使うとよいと思います。 別のページで述べることになりますが，ヤング率も圧力と同じ単位で ［ＧＰａ］がよく使われます。それぞれの単位換算を表１に示します。