体積ひずみ，体積弾性係数

ＨＯＭＥ　＞　材料力学　＞　体積ひずみ，体積弾性係数

体積ひずみ

物体が外力を受けて変形し体積が変化したとき，変形前の体積をＶ，変形による体積変化量をΔＶとすれば，体積ひずみε_ｖ(volumetric strain)は次式で定義されています。

図１に示すように，一辺の長さがａの立方体の各面に垂直応力σ１，σ２，σ３が作用して，各辺の長さがａ（１＋ε１），ａ（１＋ε２），ａ（１＋ε３）に伸びたとします。

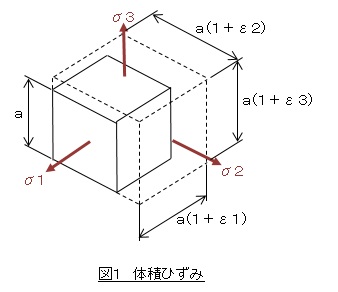
このときの体積ひずみを求めましょう。

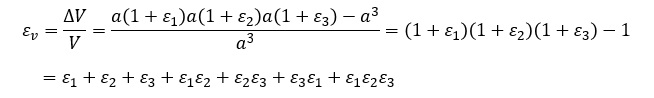
弾性変形のひずみεは０．００１[-]以下と小さい値なので，ε１ε２　など二次以上の微小項をゼロとおいて

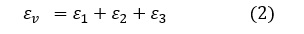
体積ひずみは縦ひずみの和に等しくなります。

体積弾性係数

直方体の各面に等しい引張ないしは圧縮応力σが作用しているときを考えます。弾性体の場合，σと体積ひずみε_ｖが比例し，その比例定数Ｋを体積弾性係数(modulus of volumetric elasticity)と言います。Ｋは次式で定義されます。

(3)式の分子の単位は[Pa]，分母は無次元量[-]なので。体積弾性係数Ｋの単位は応力と同じ[Pa]となります。

ＳＳ４００のＫをヤング率Ｅとポアソン比νから求めてみましょう。Ｋ，Ｅ，νには，次式の関係があります。

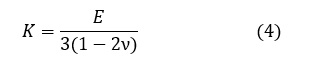
数値を代入しましょう。172[GPa]になりました。

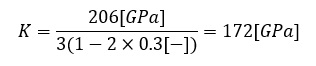
参考文献

１）中山秀太郎，大学課程　材料力学，オーム社，(S53)

２）日本機械学会，機械工学便覧　Ａ４　材料力学，(1992)