自重がかかる片持ちはり

ＨＯＭＥ　＞　材料力学　＞　自重がかかる片持ちはり

自重がかかる片持ちはりのたわみ量と応力を紹介します。有限要素法ソフトの動作確認やソフトに入力する材料定数の単位系の確認などに使用してください。

先端のたわみ量

図１に示すような，自重が作用する片持ちはりを考えます。

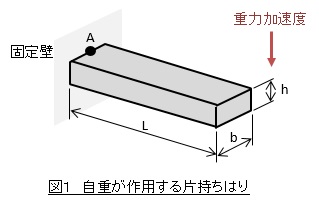
寸法は以下の通りとします。

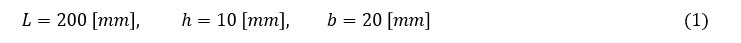
ヤング率Ｅ，密度ρ，重力加速度gは以下の値とします。

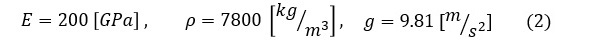
まず断面二次モーメントＩを求めます。計算はＳＩ単位系で行います。長さは[m]，力は[N]，ヤング率は[Pa]を使います。また，有効数字は３桁で計算します。

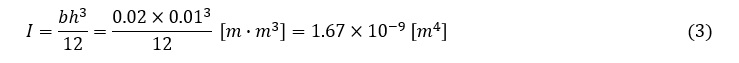
単位長さ当たりの荷重wを求めます。wは次式で求まります。

先端のたわみδは次式で求まります。

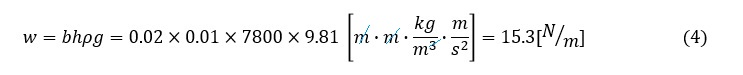
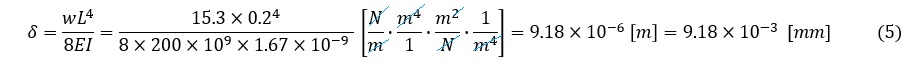
最大応力値

最大の曲げ応力は，曲げモーメントＭが最大となるＡ点で発生します。Ａ点の曲げモーメントＭは次式で求まります。

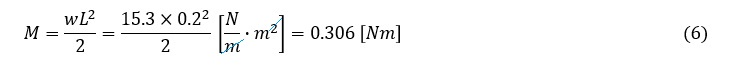
最大の曲げ応力σは次式で求まります。

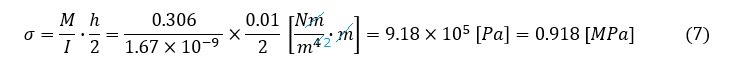
有限要素法による計算結果

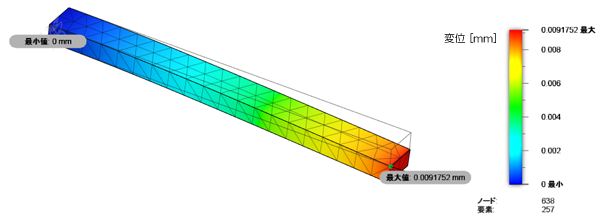
上記問題を有限要素法で解いてみました。変位図を図２に示します。先端のたわみは9.18 x 10^-3[mm]となりました。

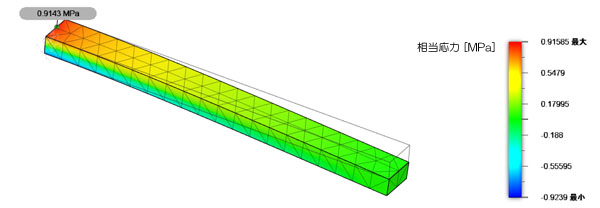
はりの長手方向（Ｘ方向）応力分布図を図３に示します。Ａ点の応力は0.914[MPa]となりました。