応力集中係数

ＨＯＭＥ　＞　材料力学　＞　応力集中係数

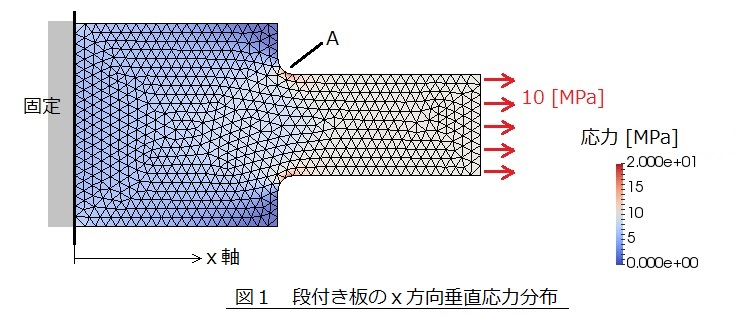
図１は段付き板の端面を10[MPa]で引張ったときのｘ方向垂直応力分布です。Ａ点で約20[MPa]と高い応力が発生しています。このように形状が急に変化する場所で高い応力が発生する現象を応力集中と言います。形状が急に変化する場所としては，切欠，穴，段，キー溝などがあります。疲労破壊は応力集中部を起点として起こりますので注意が必要です。材料欠陥部も応力集中が発生しますのでこれも疲労破壊の起点となります。

次式で定義される係数を応力集中係数(stress concentration factor)とか形状係数(form factor)と言います。

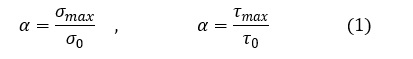
σｍａｘ，τｍａｘは，応力集中部の最大垂直応力ないしは最大せん断応力です。σｏ，τｏは基準応力と言い，応力集中が生じないとして計算される公称応力です。応力集中係数を扱う場合，基準応力としてどの断面に基づいて計算されたものかを明確にしておく必要があります。多くの場合，最小断面積に基づいて計算される応力ですが，そうでない場合も場合もありますので，文献を参照する際は基準応力の定義を注意深く読んでおく必要があります。

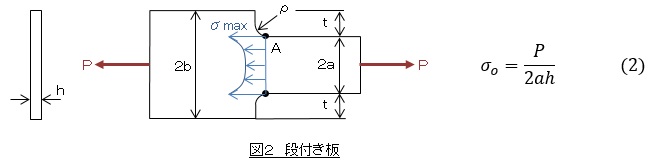
図２に示すような段付き板に引張り荷重Ｐが作用している場合の応力集中係数αを例にとります。段の部分には曲率半径ρのコーナＲがあるとします。最大応力σｍａｘはＡ点近傍で発生します。基準応力σｏは断面が小さい側の公称応力として(2)式で定義します。応力集中係数αは図３のようになります。

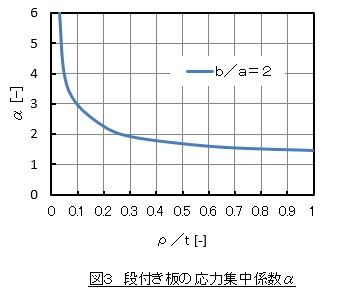
応力集中係数αの特徴は，ρがゼロに近づくとαが急に大きくなることです。よって，機械の設計では可能な限りρ（コーナＲ）を大きくとることが重要になります。

図１の例は，ｂ＝20[mm]，ａ＝10[mm]，ρ＝３[mm]でした。ρ／ｔ＝0.3[-]なのでα＝約2[-]となり，最大応力σｍａｘは20[MPa］となります。図１の結果もＡ点の応力は約20[MPa]だったので両者は一致していますね。このように，有限要素法を使ってαを簡単に求めることができます。

疲労破壊の有無の予測では，応力拡大係数αの代わりに切欠係数βを使うことになっていますが，αが３より小さい場合はα＝βとおいてαを使うことができます。つまり有限要素法を使って求めた応力と疲労強度を比較して，疲労破壊の有無を予測できます。αが３より大きな場合にこの方法を使うとオーバースペック気味の設計となり不経済です。このような場合は公称応力ベースの疲労評価が必要になります。

ρがゼロの場合のＡ点を応力特異点と言います。αは無限大になります。有限要素法で応力特異点の応力を計算したら，要素分割を変えると応力値も変化し，応力が一義的に定まりません。応力特異点がある場合も公称応力ベースの疲労評価をすることによりこの問題を解決できます。

参考文献

日本機械学会，機械工学便覧　Ａ４　材料力学，(1992)