平面応力状態の主応力

ＨＯＭＥ　＞　材料力学　＞　平面応力状態の主応力

二次元で考えた主応力，つまり平面応力状態での主応力は，計算力学技術者（ＣＡＥ技術者）の資格認定試験では出てきますので，ここで述べておきます。

平面応力では，σｘ，σｙ，τｘｙがある値を持っています。σｚ，τｙｚ，τｚｘはゼロです。

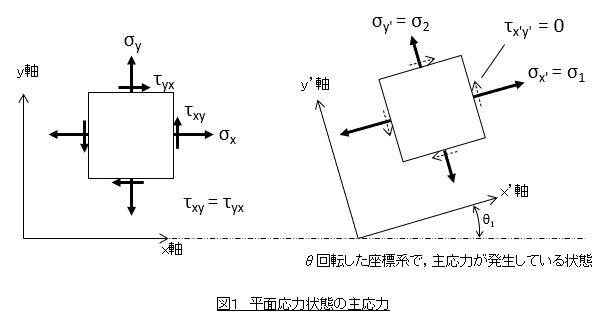
図１を用いて説明します。図の左側は応力（σｘ，σｙ，τｘｙ）が作用している状態です。図の右側は。座標系を上手に回転して，回転後のせん断応力τｘ’ｙ’をちょうどゼロにした状態です。そのときの垂直応力（σｘ’，σｙ’）が主応力（σ１，σ２）です。

別の表現をします。σｘ’は回転角θの関数です。σｘ’＝ｆ（θ）としましょう。θを０°から１８０°まで変化したときに，σｘ’は最大値と最小値をとります。この最大値がσ１，最小値がσ２です。τｘ’ｙ’もθの関数ですが，σｘ’が最大値と最小値をとるとき，τｘ’ｙ’はゼロになります。

主応力は次式で計算できます。

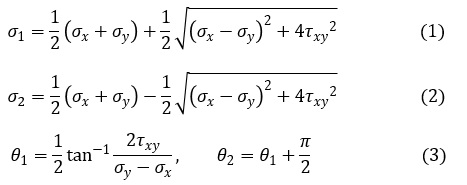
平面応力状態の主せん断応力

主せん断応力を説明します。τｘ’ｙ‘も回転角θの関数です。τｘ’ｙ‘＝ｇ（θ）としましょう。θを０°から１８０°まで変化したときに，τｘ’ｙ‘は最大値と最小値をとります。この最大値がτ１，最小値がτ２です。次式で表されます。

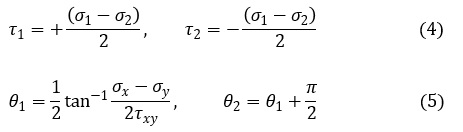
主せん断応力が発生する方向は，主応力が発生する方向を４５°回転した方向です。