主応力

ＨＯＭＥ　＞　材料力学　＞　主応力（三次元版）

有限要素法ソフトで表示される応力

有限要素法で応力分布図を表示するとき，いろいろな選択肢があります。以下のようなものです。

• σｘ（ｘ成分垂直応力），σｙ（ｙ成分垂直応力），σｚ（ｚ成分垂直応力），
  τｘｙ（ｘｙせん断応力），τｙｚ（ｙｚせん断応力），τｚｘ（ｚｘせん断応力）

• σ１（第一主応力），σ２（第二主応力），σ３（第三主応力）

• σｅｑ（相当応力，ミゼス相当応力）

二番目のσ１，σ２，σ３（主応力）を説明します。

材料力学を履修した人は，平面応力状態の主応力（二次元版主応力）を習ったと思いますが，ＣＡＥを使った設計現場では三次元ＣＡＤから形状データを有限要素法ソフトにインポートして三次元解析をするのがほとんどなので，ここでは三次元版主応力を説明します。しかし，計算力学技術者の資格認定試験（２級）では二次元版（平面応力）の主応力が出題されることが想定されるため，別のページで説明します。

三軸応力

三次元版主応力の説明の前に，三軸応力のページを読んでください。

着眼している立方体を傾けてみる

図１を見てください。左側は応力を考える際に着眼している立方体の各辺がｘ軸，ｙ軸，ｚ軸と平行な場合です。この場合の応力成分は，σｘ，σｙ，σｚ，τｘｙ，τｙｚ，τｚｘです。図１の右側は着眼している立方体を傾けた場合です。このときの座標軸をｘ’軸，ｙ’軸，ｚ’軸，応力をσｘ’，σｙ’，σｚ’，τｘ’ｙ’，τｙ’ｚ’，τｚ’ｘ’とします。これから，立方体を傾けたときの応力を考えていきます。

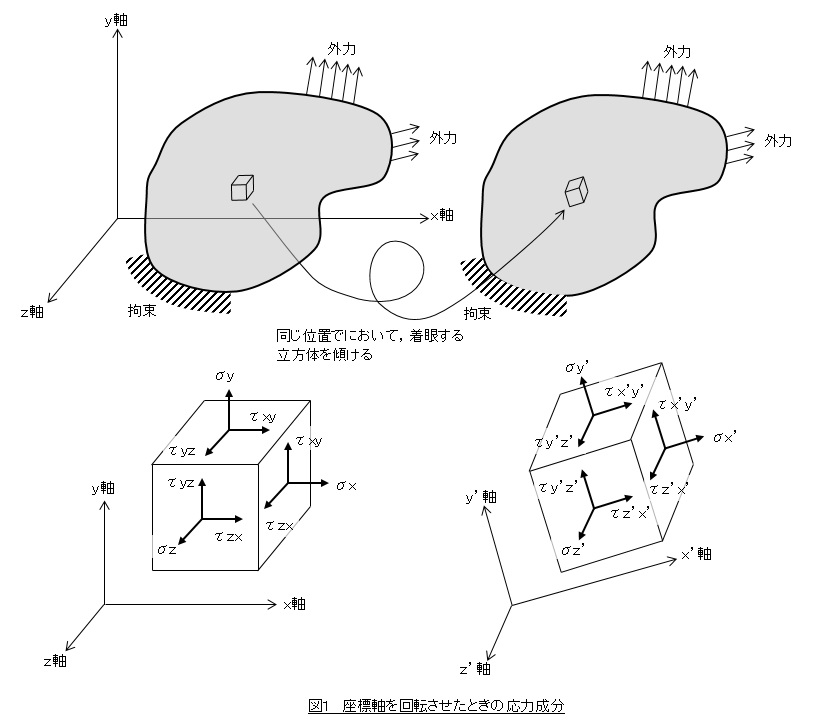
方向余弦を使った立方体を傾けた量の表現

ｘ’ｙ’ｚ’直交座標系がｘｙｚ直交座標系に対してどけだけ回転したかを，方向余弦で表現します。

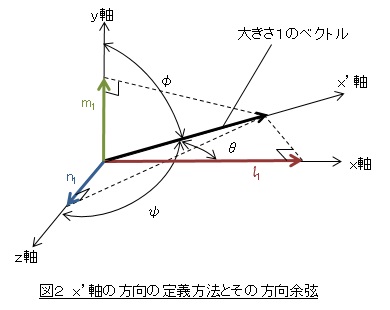
図２に，ｘ軸，ｙ軸，ｚ軸とｘ’軸の関係を示します。絵を単純にするためｘ’軸だけ書いています。ｘ’軸とｘ軸とのなす角をθ，ｘ’軸とｙ軸とのなす角をφ，ｘ’軸とｚ軸とのなす角をψとします。これでｘ’軸の方向が定義できました。

図２において，ｘ’軸を向き大きさ１のベクトルと考えます。このベクトルのｘ方向成分をl₁（エルいち），ｙ方向成分をm₁，ｚ方向成分をn₁と表記します。（l₁,m₁,n₁)をｘ’軸の（ｘ，ｙ，ｚ）への方向余弦と言います。

（l₁,m₁,n₁)は次式で表されます。

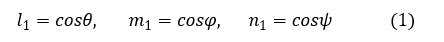
同様の発想で，ｙ’軸の（ｘ，ｙ，ｚ）への方向余弦（l₂,m₂,n₂)と，ｚ’軸の（ｘ，ｙ，ｚ）への方向余弦（l₃,m₃,n₃)を定義します。以下のように９つの方向余弦成分で定義できました。

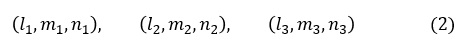
方向余弦成分が９つあると書きましたが，実は３つだけ決まれば残り６個は計算して求まります。独立変数は３つということです。

応力成分の座標変換

回転したｘ’ｙ’ｚ’直交座標系の応力成分の計算方法を説明します。σｘ，σｙ，σｚ，τｘｙ，τｙｚ，τｚｘと，σｘ’，σｙ’，σｚ’，τｘ’ｙ’，τｙ’ｚ’，τｚ’ｘ’の関係は次式となります。

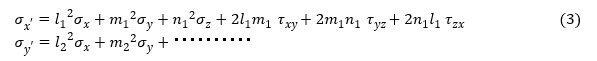
式で書くとみずらくなるため，行列式で表現しました。次式となります。

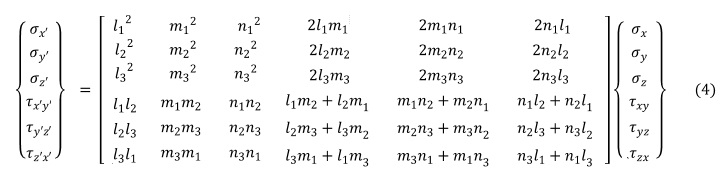
主応力（principal stress）

上手にｘ’軸，ｙ’軸，ｚ’軸の方向を決めると，τｘ’ｙ’，τｙ’ｚ’，τｚ’ｘ’が同時にゼロとなる組合せがいくつかあります。このときのσｘ’，σｙ’，σｚ’を大きいものからσ１，σ２，σ３と表記します。σ１を第一主応力（最大主応力），σ２を第二主応力（中間主応力），σ３を第三主応力（最小主応力）と言います。そしてこのときのｘ’軸，ｙ’軸，ｚ’軸を主応力軸ないしは応力の主軸と言います。また，ｘ’軸，ｙ’軸，ｚ’軸を向いた立方体の面を主応力面と言います。

ｘ’軸，ｙ’軸，ｚ’軸の方向を変えるとσｘ’，σｙ’，σｚ’が変化しますが，その最大値はσ１より大きくなりません。つまりσ１がσｘ’，σｙ’，σｚ’がとりうる値の最大値です。また，σ３がσｘ’，σｙ’，σｚ’がとりうる値の最小値です。

個人的には，最大主応力と呼ばずに第一主応力と呼んでいます。理由は，「第一主応力の最大値」といういい方はピンときますが，「最大主応力の最大値」といういい方では何の最大値かピンとこないからです。

プラスの応力は引張応力なので，多くの場合第一主応力σ１は引張応力となり，マイナスの応力は圧縮応力なので，第三主応力σ３は圧縮応力となります。

主応力の計算方法

σ１，σ２，σ３は，次式で示す三次方程式の３根であり，エクセルを使って求めることができます。三次元版主応力を求めるエクセルシートを作成しました。ここをクリックしてみてください。

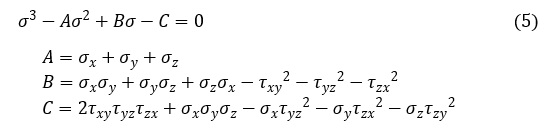
(5)式を行列式で表現すると，次式となります。

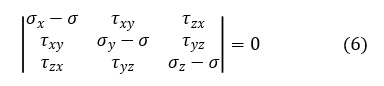
主応力の用途

有限要素法で求まる応力はσｘ，σｙ，σｚ，τｘｙ，τｙｚ，τｚｘの６つなのですが，この内のどの応力成分を引張強さσ_Ｂや降伏応力σ_ｙと比較すればよいかはわかりませんね。主応力を簡単に言うと，「６つの応力成分を代表してひとつの応力値」としたものと解釈できます。代表として使うものは第一主応力（最大主応力）σ１です。正確には，主応力は最大主応力説に従って機械や構造物が破損（塑性変形や破壊）するかどうかを判断するときに使います。

また，疲労破壊するかどうかの検討では，最大応力と最小応力から平均応力と応力振幅を求めるのですが，最大応力を「最大応力が発生するような荷重条件で解析した結果」の第一主応力σ１とし，最小応力を「最小応力が発生するような荷重条件で解析した結果」の第三主応力σ３とする方法が考えられます。厳密にはσ１の方向とσ３の方向が一致していないのですが，厳しめの評価（安全側の評価）となりますので，複雑な応力が発生している場合，つまりσｘ，σｙ，σｚ，τｘｙ，τｙｚ，τｚの６つが同時に発生している場合に有効だと思います。

参考文献

材料力学ハンドブック（基礎編），日本機械学会，丸善，(1999)