主せん断応力

ＨＯＭＥ　＞　材料力学　＞　主せん断応力（三次元版）

主応力

三次元版主せん断応力の説明を読むの前に，三軸応力のページと主応力のページを読んでください。

主せん断応力

図１に示すように，着眼している立方体の方向を変えればその立方体に作用する応力成分がかわります。

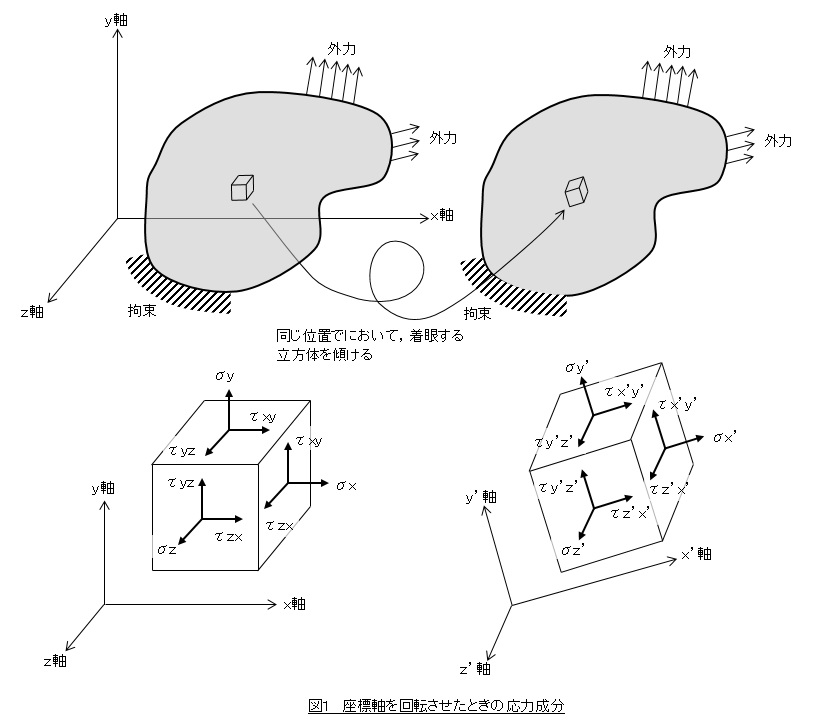
ｘ’ｙ’ｚ’軸の方向をうまく選べば，τｘ’ｙ’が最大になる方向があります。また，τｙ’ｚ’が最大になる方向とτｚ’ｘ’が最大になる方向もあります。このような方向のせん断応力を主せん断応力と呼びます。

主せん断応力をτ１，τ２，τ３と表記すれば，次式で表されます。ここでσ１，σ２，σ３は主応力です。

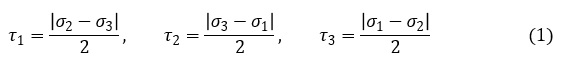
主せん断応力が発生する方向を説明します。τｘ’ｙ’とτｙ’ｚ’とτｚ’ｘ’が同時に最大となるわけではなく，別々の方向でそれぞれが最大になります。今，ｘ’ｙ’ｚ’軸が主応力を発生させる方向とします。立方体をｘ’軸を中心に４５°回転したときの立方体の６面のうち２面に，τ１，τ２，τ３のうち１つが発生しています。残り４面のせん断応力はゼロです。次に，立方体をｙ’軸を中心に４５°回転ときの立方体の６面のうち２面にτ１，τ２，τ３のうち次の１つが発生しています。最後に，立方体をｚ’軸を中心に４５°回転ときの立方体の６面のうち２面にτ１，τ２，τ３のうち最後の１つが発生しています。そして，主せん断応力が発生している方向での垂直応力σｘ’，σｙ’，σｚ’はゼロではありません。

主せん断応力の用途

有限要素法で求まる応力はσｘ，σｙ，σｚ，τｘｙ，τｙｚ，τｚｘの６つなのですが，この内のどの応力成分をせん断強さτ_Ｂやせん断降伏応力τ_ｙと比較すればよいかはわかりませんね。主せん断応力を簡単に言うと，「６つの応力成分を代表してひとつの応力値」としたものと解釈できます。代表として使うものはτ１，τ２，τ３の最大値です。正確には，主せん断応力は最大せん断応力説に従って機械や構造物が破損（塑性変形や破壊）するかどうかを判断するときに使います。