相当応力，ミゼス相当応力

ＨＯＭＥ　＞　材料力学　＞　相当応力，ミゼス相当応力

有限要素法ソフトで表示される応力

有限要素法で応力分布図を表示するとき，いろいろな選択肢があります。以下のようなものです。

• σｘ（ｘ成分垂直応力），σｙ（ｙ成分垂直応力），σｚ（ｚ成分垂直応力），
  τｘｙ（ｘｙせん断応力），τｙｚ（ｙｚせん断応力），τｚｘ（ｚｘせん断応力）

• σ１（第一主応力），σ２（第二主応力），σ３（第三主応力）

• σｅｑ（相当応力，ミゼス相当応力）

三番目のσｅｑ（相当応力，ミゼス相当応力）を説明します。

三軸応力

三次元版主応力の説明の前に，三軸応力のページを読んでください。

相当応力，ミゼス相当応力

有限要素法で応力を計算したら，６つの応力成分（σｘ，σｙ，σｚ，τｘｙ，τｙｚ，τｚｘ）が求まります。せん断ひずみエネルギ説という考え方を用いて，この６つの応力成分を代表してひとつの応力として表したものが，相当応力(equivalent stress)です。ミゼス相当応力とも言います。

６つの応力成分を示されたとしても，解析対象が降伏（塑性変形）するかどうかは判断が難しいですね。しかし，有限要素法ソフトが出力する相当応力σｅｑを使うことによって，材料が降伏したかどうかがわかります。相当応力が降伏応力σｙ以上になっていればその材料は降伏していることになります。

相当応力は次式で計算します。

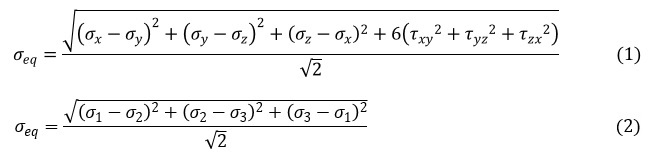
ここで，σ１，σ２，σ３は主応力です。

式の形からわかるように相当応力はプラスの値しか持ちません。圧縮応力が作用しているときでもプラス値となります。この点に注意する必要があります。例えば大きな圧縮応力が発生している点があったとします。延性材料の場合圧縮応力なら少々大きくても設計変更の必要はありませんね。しかし相当応力だけを見ているとプラスの大きな値が出力され，設計変更の必要ありと判断されてしまう危険性があります。必ずしも相当応力が大きいからと言って設計変更する必要があるわけではないのです。相当応力が大きい点については，主応力を見てその点が圧縮応力状態か引張応力状態かを見極める必要があります。

相当応力の意味を理解するために，例を示しましょう。
今，降伏応力σｙが200[MPa]の材料があったとします。二つのケースを比較します。

　ケースＡ：σｘ=150[MPa]，σｙ=150[MPa]，σｚ=150[MPa]，τｘｙ=τｙｚ=τｚｘ=0[MPa]

　ケースＢ：σｘ=150[MPa]，σｙ=-150[MPa]，σｚ=-150[MPa]，τｘｙ=τｙｚ=τｚｘ=0[MPa]

どちらのケースも150[MPa]の応力が作用していますがσｙとσｚの符号が違います。150[MPa]と降伏応力200[MPa]より小さな値なので，降伏しないような感じですがどうでしょうか。この応力状態で降伏するかどうか，(1)式に数値を代入して相当応力を使って調べましょう。相当応力は以下のようになります。

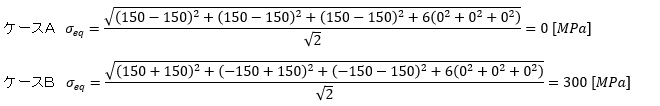
ケースＡの相当応力は0[MPa]となって全く降伏しない結果となり，ケースＢの相当応力は300[MPa]となり降伏するという結果となりました。図１を使って説明しましょう。

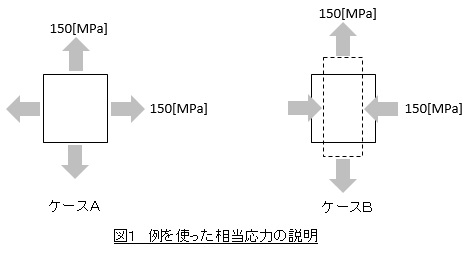
ケースＡはあらゆる方向から引張られており変形しようがないのです。このような場合変形していないのだから相当応力は小さな値となります。一方ケースＢは，上下方向に引張られて縦長に変形しているのですが，水平方向では圧縮されて縦長に変形するのを助長しております。ケースＢは単に上下に引張られているよりより大きく変形しているので相当応力は大きくなります。以上のように相当応力は物体の変形の大きさを表す量なのです。

相当応力の用途

厳密には相当応力は，せん断ひずみエネルギ説に従って機械や構造物が降伏するかどうかを判断するときにを使います。

しかし，有限要素法による応力計算結果の全体像をざっと見るとき，疲労強度σｗを比較して疲労破壊の有無を予測するとき，引張強さσ_Ｂと比較して破断するか予測したいときなどにも使われています。σｗやσ_Ｂとの比較は相当応力の守備範囲から外れているように思われますが，多くの用途に非常によく使われている現実があります。

疲労破壊の有無を予測するときの注意点を述べます。疲労破壊の有無の予測には応力振幅を求めます。応力振幅は次式で計算します。

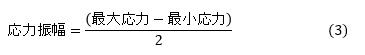
例えば，単軸応力下（σｘしか発生していない応力場）において，最大応力が30[MPa]，最小応力が-10[MPa]だったとします。応力振幅は　(30-(-10))/2=20 [MPa]　ですね。しかし，相当応力を使うと最小応力が-10[MPa]ではなく+10[MPa]となって，応力振幅は　(30-10)/2=10 [MPa]　と小さく計算されてしまいます。応力振幅を小さく見積ってしまうことは，「壊れるかもしれないもの」を「壊れないと」と判断してしまう危険性があります。応力振幅の計算には主応力を使うべきです。