ひずみとポアソン比

ＨＯＭＥ　＞　材料力学　＞　ひずみとポアソン比

垂直ひずみ

図１に示すように，初期長さＬ，初期直径ｄの丸棒が荷重Ｐで引張られていて，長さがΔＬだけ伸びて直径がΔｄだけ縮んだとします。

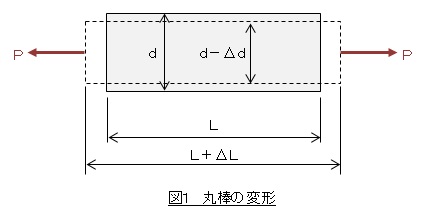
縦ひずみε(longitudinal strain)と横ひずみε_Ｌ(lateral strain)は次式で定義されています。

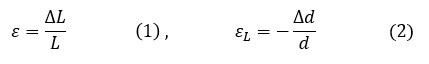
縦ひずみのことを垂直ひずみ(normal strain)とか，単にひずみ(strain)と呼びます。

ひずみの符号は，物体が伸びたときをプラス，縮んだときをマイナスとします。(2)式では直径が縮んでいるのでマイナスの符号をつけました。

せん断ひずみ

図２に示すように，直方体にせん断荷重Ｐが作用し，四角形ＡＢＣＤが平行四辺形ＡＢＣ’Ｄ’に変形したとします。ここで点Ｂと点Ｃの距離Ｌは極めて小さいとします。

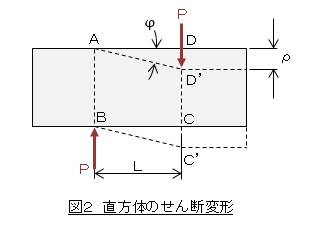
せん断ひずみγ(shearing strain)は次式で定義されています。

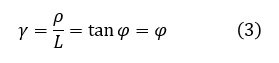
φの単位はラジアンです。弾性変形域でのγは0.001[-]と微小なので，ｔａｎφ＝φとしました。

ひずみの単位

(1)，(2)，(3)式では長さを長さで割っていますので，ひずみの単位は無次元量となります。[-]と表記します。パーセント[%]で表記されることもあります。[με]という単位が使われることがありますが，１[με]は１×１０^－６[-]です。

(3)式においてラジアン[rad]が登場しますが，ラジアンの定義は　円弧の長さ÷半径　なので無次元量[-]です。

ポアソン比

図１の状態で，横ひずみε_Ｌを縦ひずみで割った値の絶対値をポアソン比ν(Poisson's ratio)と言います。式で表すと以下のようになります。

体積変化がないときのポアソン比νを計算してみましょう。

変形前後の体積が等しいとして，次式が成立します。

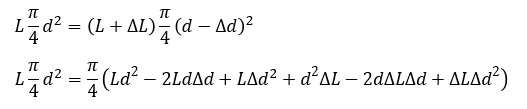
ΔＬとΔｄは微小であるため，２次以上の微小項をゼロとして

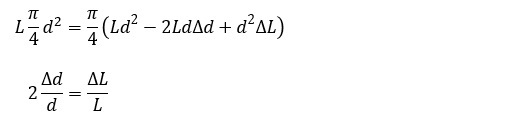
(1)式と(2)式を代入して

(4)式から

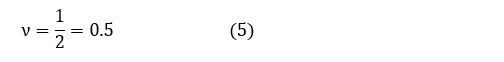
体積変化がないときのポアソン比νは０．５[-]となります。しかし，有限要素法ソフトにν＝０．５[-]を入力すると，体積弾性率が無限大となってエラーとなってしまいますので注意が必要です。金属材料のポアソン比は０．３[-]程度の値です。弾性変形の場合，図１のように引張ったときは体積が増加し，圧縮したときは体積は減少します。ポアソン比が０．５[-]より小さいの値をとることは，引張ったり圧縮したりしたときに体積変化があることを意味します。

主な金属のポアソン比をＥ，Ｇ，ν，Ｋの関係のページに記します。