要素分割の細かさの確認，メッシュスタディ

ＨＯＭＥ　＞　Ｖ＆Ｖ　＞　要素分割の細かさの確認

Ｖ＆Ｖの検証工程において要素分割の細かさが適切であったかどうかをチェックすることはとても大事なことです。一般的に要素分割が粗いと変位と応力は低めに出力されるので，要素分割が粗い計算結果を採用した設計は危険な設計となります。

要素分割と解析精度では，要素分割を細かくすれば計算結果は弾性力学による厳密解に近づくと述べました。一方，要素サイズを半分にすると要素数は約８倍になり，計算時間が急激に長くなります。どこかで折り合いをつけなければなりません。その手順を実施例とともに説明します。

手順

下記手順で要素分割の細かさの確認を行います。

• ①必ず２次要素を使っていることを確認しておく。もはや１次要素は時代遅れです。

• ②ある要素サイズ（有限要素法ソフトのディフォルトの要素サイズでいいでしょう）で計算し，注目している点（応力集中部が適切です）の応力を読取る。

• ③要素サイズを半分にして同様の計算をし，応力値を読取る。

• ④　②の結果と③の結果の差を計算する。

• ⑤差が５％以下になるまで③と④の作業を繰り返す。

• ⑥強度計算において，応力計算結果が数％低いことに対する安全率を追加する。

上記⑥を追加した理由は，差が５％以下だからといって計算結果が十分厳密解に近い保証がないからです。要素分割が粗いと応力は低めに出力されるので，その分を設計マージンに加える必要があります。

実施例

図１に示すようなだ円孔を持つ板が左右方向に引張られるケースを例にとって，要素分割の細かさの確認を行いましょう。Ａ点の応力に注目します。

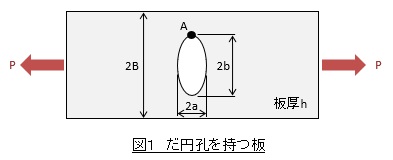
寸法と荷重Ｐは以下とします。

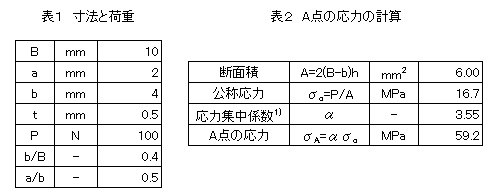
参考までにＡ点の応力の弾性力学的な解を求めておきましょう。応力集中係数αは文献¹⁾からα＝3.55[-]なので，Ａ点の応力は表２に示すように59.2[MPa]となります。

要素サイズ1.0[mm]で計算しました。要素分割図を図２に示します。Ａ点の応力は45.5[MPa]となりました。

次に要素サイズ0.5[mm]で計算しました。要素分割図を図３に示します。Ａ点の応力は57.9[MPa]となりました。

要素サイズ1.0[mm]の計算結果とのＡ点の応力の差は次式に示すように23.9[%]となり，５[%]より大きくなりました。あと１回要素サイズを半分にして計算する必要があります。

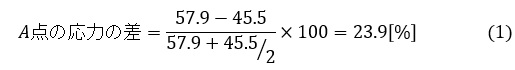
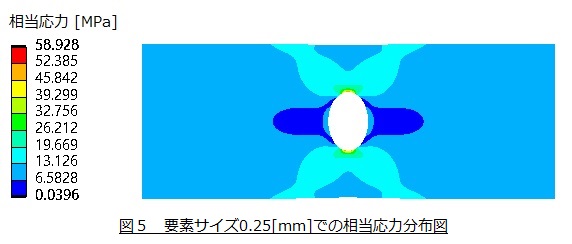
要素サイズ0.25[mm]で計算しました。要素分割図を図４に，相当応力図を図５に示します。Ａ点の応力は58.2[MPa]となりました。図５のコンタ図では最大値が58.928[MPa]となっていますが，先ほど述べた値（58.2[MPa]）と少し異なります。先ほど述べた値は，Ａ点に相当する節点が複数個ありその節点での値の平均値であります。

Ａ点の応力の差は次式に示すように0.5[%]となり，5[%]より小さくなりました。応力計算はこれで終了です。

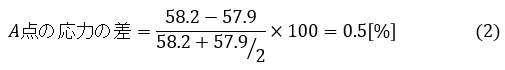
ここで注意したい点があります。Ａ点の応力の最後の計算結果は57.9[MPa]，厳密解は59.2[MPa]で1.6[%]だけ計算結果の方が小さいです。今回は厳密解がわかっている問題を解きましたので計算結果がどれだけ小さいかがわりましたが，通常の設計業務ではどれだけ小さいかはわかりません。そのために安全率があるのです。安全率を構成するアイテムの一つに「応力計算の不確からしさ」に関する項を入れる必要があります。数[%]くらいでよいのでしょうがこの値は各自の責任で決めてください。

コメント

多くの有限要素法ソフトでは上述した作業を自動で行う機能がありますので積極的に使ってみてください。ただし，繰返し計算になりますので計算打ち切り判定値を小さくすると計算が終わらないことがありますので注意してください。

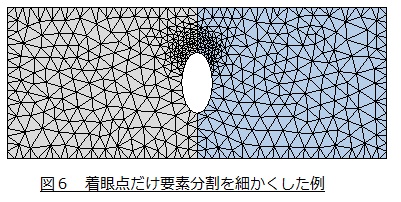
今回の検討結果ではかなり細かい要素分割になりました。要素分割の細かさの確認作業では，小さい要素となりますので要素数がとても多くなって計算時間がかかります。非線形解析でこれをやったら気が遠くなるような計算時間となるでしょう。この対策として，着眼点だけ要素分割を細かくする方法があります。例を図６に示します。

参考文献

１）日本機械学会，機械工学便覧　A4　材料力学，p76，(1984)

２）泉，酒井，理論と実践がつながる　有限要素法シミュレーション，森北出版，(2010)